Inscription / Connexion Nouveau Sujet
filtre ACTIF par AOP
Bonjour,
je souhaiterai avoir quelques conseils et correction sur ce montage (considerant AOP IDEAL).
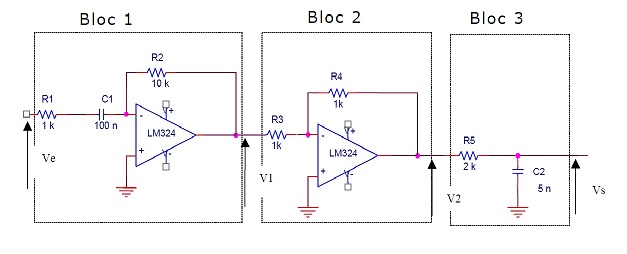
pour le BLOC I:
Exprimez la relation du module de T1(w)
je trouve une fct de transfert tel que équivalente à un Filtre passe haut :
par Millman je trouve T= - R2/Z1
-(R2JCW)/(R1JCW+1)
avec 1/R1C= w1=10000
et 1/R2C= w2=1000
Soit T(jw)= -(jw/w2)/(1+j(w/w1))
ce qui me gene, c'est le moins(-), dois je m'en affranchir? et alors comment calculer le gain,la phase,
dois calculer un filtre passe haut classique en demontrant les differentes tendence
20db/dec qd w->0
0db qd w->oo
auquel j'ajoute le module de |R2/R1| 20Log(10)= 20db aVec dephasage de 180°
Je ne sais pas trop comment m'y prendre
- Exprimez la relation de G1 gain de T1(w)
|-(R2/R1)|=10
par avance, merci
Apres "prise de tete" avec mon signe (-)...j'ai pris le probleme de façon simple sans me poser de question et j'obitens ceci:
en reprenant ici:
par Millman je trouve = - R2/Z1
v1/ve= T1(w)= -(R2JCW)/(R1JCW+1)
avec 1/R1C= w1=10000
et 1/R2C= w2=1000
Soit T1(jw)= -(jw/w2)/(1+j(w/w1))
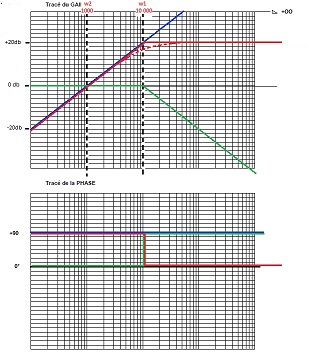
en terme de MODULE: |T1|= sqrt[(w/w2)²]/sqrt[(1+(w/w1)²]
GAIN
G1|T1|= 20 log (w/w2) - 20 log[sqrt[(1+(w/w1)²]]
= 20 log (w/w2) - 10 log[(1)²+(w/w1)²]
= 20 log (w/w2) - 10 log[ 1+(w/w1)²]
pente +20db (bleu) et pente de - 20db (vert)
PHASE
1= Arg(jw/w2) - Arg(1+jw/w1)
/2 - tan-1(w/w1)
(bleu) - (vert)
tracé asymptotique (joint) pour la totalité de T1
GAIN G1 (rouge sur diagramme)
pente de + 20db de 0 jqa la valeur particuliere de W1 puis droite jqa l'infini à +20db
PHASE 1 (rouge sur diagramme)
/2 de 0 jusqu'à la valeur particuliere de W1 puis 0° de W1 à +
------------------------------------------------------------------------------------------------
Ma question:
puisque la fct de transfert est negative, donc inverse ce qui implique un dephasage de 180°
ne dois pas en plus ajouter ce dephasage sur l'ensemble du BLOC 1 ?
soit :
+ /2 - tan-1(w/w1)
Annuler
connectez vous