bonjour

recopie ton énoncé, stp

Philoux

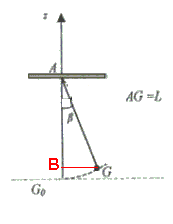
On étudie un pendule simple constitué d'une masse ponctuelle m, attaché à l'une des extrémités d'un fil inextensible, de masse négligeable et de longueur L
Ce pendule est placé dans le champ de pesanteur dans le référentiel terrestre considéré comme galilien.

Etude énergirique
-Donner l'expression de l'énergie cinétique en G
-On prendra l'origine des énergie potentielles en G0, origine de l'axe des z
-On montre que dans ce cas l'énergie potentille en G peut se mettre sous la forme Ep=mgl(1-cosbéta)
-Donner l'éxpression de l'énergie mécanique en fonction de m g L et béta
-Pourquoi l'énergie mécanique se conserve-t-elle ?
-Exprimer la vitesse au passage par la position d'équilibre en fonction de g L et Bétam
-Calculer sa valeur
Données : g=10m/s L=1 m  cos béta= 0,95

Avec v la vitesse de la masse pour l'angle beta.

Energie cinétique = (1/2).m.v²
Energie potentielle = mgL(1-cos(beta))

Energie mécanique = (1/2).m.v² + mgL(1-cos(beta))

L'énergie mécanique se conserve parcequ'il n'y a pas de frottement dans l'air (masse ponctuelle).
----
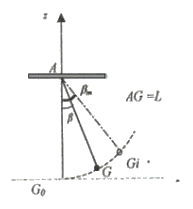
Si beta = beta_max, v = 0 -->
Energie mécanique = (1/2).m.v² + mgL(1-cos(beta))
Energie mécanique = mgL(1-cos(beta_max))

On a donc pour tout angle beta dans [-beta_max ; beta_max]:
mgL(1-cos(beta_max)) = (1/2).m.v² + mgL(1-cos(beta))

gL(1-cos(beta_max)) = (1/2).v² + gL(1-cos(beta))
-gl.cos(beta_max)) = (1/2).v² -gl.cos(beta))

v² = 2gl(cos(beta) - cos(beta_max))



en position dite d'équilibre, et on a alors:





C'est la vitesse de la masse aux passages par la position d'équilibre.
-----
Sauf distraction.  

Bonjour !

Désolé de ressortir un aussi vieux topic, mais j'ai à peu près le même devoir. Seulement, à la place de "On montre que dans ce cas l'énergie potentille en G peut se mettre sous la forme Ep=mgl(1-cosbéta)", j'ai "montrer que..." et je ne sais pas du tout comment faire !
Merci d'avance.

AB = AG.cos(beta)

BGo = AGo - AB
Or AGo = AG = L -->

BGo = L - L.cos(beta)
BGo = L(1-cos(beta)
---
Ep = mgh avec h la différence d'altitude entre le centre d'inertie de la masse lorsque la corde fait avec la verticale un angle beta et lorsqu'elle fait un angle = 0.

--> Ep = mg.BGo
Ep = mgL(1-cos(beta))
-----
Sauf distraction.  

Zut, j'ai oublié le dessin, le voici:

Merci beacoup, c'est très clair

Bonjour, j'ai le même dm et j'ai du mal à comprendre votre réponse où vous calculez la vitesse,
comment peut-on dire que béta=béta_max et donc que v=0 ?
De quelle vitesse parlez-vous ? car après on calcule une autre vitesse qui est égale à 1m.s-1 ...