Inscription / Connexion Nouveau Sujet
etude de deux modeles d'oscillateurs
bonsoir a tous je bloque dans un exercice de phisique
pouvaix vous m aider svp ?
On se propose d'étudier les analogies entre un oscillateur électrique et un oscillateur mécanique.
On considère les deux dispositifs suivants :
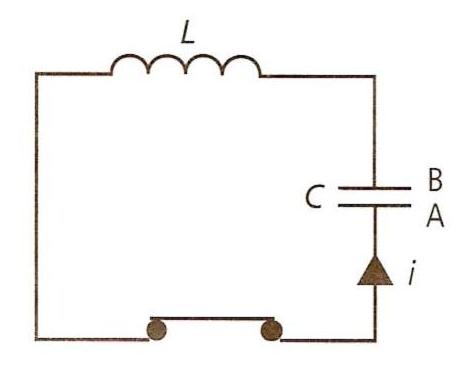
-un circuit électrique comprenant: une bobine d'inductance L, de résistance nulle, un condensateur de capacité C et un interrupteur.
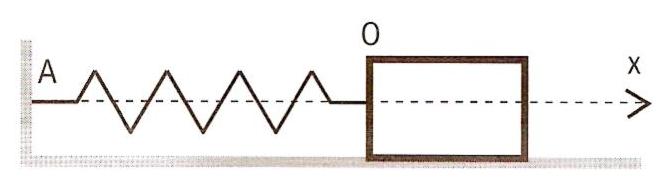
-un système solide-ressort horizontal comprenant : un solide de masse m glissant sans frottement le long d'un axe horizontal Ox ; un ressort à spires non jointives de constante de raideur k dont l'une des extrémités est attaché au solide de masse m et dont l'autre extrémité est fixée rigidement à un support fixe.
(voir les images plus bas).
A. Etude du comportement temporel des deux modèles d'oscillateurs :
1)Etablir l'équation différentielle régissant le "comportement temporel de la charge" q(t) du condensateur. En utilisant les conditions initiales, en déduire l'expression de q(t). Donner l'expression de la période T0 de cet oscillateur.
2)Etablir l'équation différentielle régissant le comportement temporel de l'élongation x(t) du ressort. En utilisant les conditions initiales, en déduire l'expression de x(t). Donner l'expression de la période T0 de cet oscillateur.
merci d avance
** énoncé effacé ; image laissée **
** énoncé effacé ; image laissée **
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
bonsoir a tous je bloque dans un exercice de phisique
pouvaix vous m aider svp ?
On se propose d'étudier les analogies entre un oscillateur électrique et un oscillateur mécanique.
On considère les deux dispositifs suivants :
-un circuit électrique comprenant: une bobine d'inductance L, de résistance nulle, un condensateur de capacité C et un interrupteur.
-un système solide-ressort horizontal comprenant : un solide de masse m glissant sans frottement le long d'un axe horizontal Ox ; un ressort à spires non jointives de constante de raideur k dont l'une des extrémités est attaché au solide de masse m et dont l'autre extrémité est fixée rigidement à un support fixe.
A. Etude du comportement temporel des deux modèles d'oscillateurs :
1)Etablir l'équation différentielle régissant le "comportement temporel de la charge" q(t) du condensateur. En utilisant les conditions initiales, en déduire l'expression de q(t). Donner l'expression de la période T0 de cet oscillateur.
2)Etablir l'équation différentielle régissant le comportement temporel de l'élongation x(t) du ressort. En utilisant les conditions initiales, en déduire l'expression de x(t). Donner l'expression de la période T0 de cet oscillateur.
je ne comprend vraiment pas et je dois le rendre binetot :S
bon aucun de vous deux n'a d'idée pour le circuit ?
Commencez par écrire la loi des mailles et essayez de trouver l'équa diff en Uc ou en i pour commencer si vous préférez
1) uc + L.di/dt = 0
i = C.duc/dt
uc + LC.d²uc/dt² = 0
q/C = uc
q/C + LC/C.d²q/dt² = 0
d²q/dt² + (1/(LC)).q = 0
apres la suite je sais pas
oui c'est bon
tu dois résoudre cette équation différentielle et trouver la période d'oscillation. Une idée ?
tu devrais être capable de trouver la période d'oscillation tout seul. Ne serait-ce que par analyse dimensionnelle.
Les solutions de cette équa diff sont de la forme :
q(t) = A.cos( o.t) + B.sin(
o.t) + B.sin( o.t)
o.t)
où  o = 2
o = 2 /To
/To
A et B sont déterminées grace aux conditions initiales
on peut faire comme ca :
v= racine carre
q(t) = A.sin(t/V(LC)) + B.cos(t/V(LC))
q(0) = Qo --> B = Qo
q(t) = A.sin(t/V(LC)) + Qo.cos(t/V(LC))
dq/dt = A/V(LC) * cos(t/V(LC)) - Qo/V(LC) * sin(t/V(LC))
i(0) = 0 ; (dq/dt)(0) = 0 ---> A/V(LC) = 0 et donc A = 0
q(t) = Qo.cos(t/V(LC))
?
et sino c est bon ?
il y a quelque chose d autre a faire ?
et comment on fait pour '' Donner l'expression de la période T0 de cet oscillateur. ''
?
2)
-k.x = m.d²x/dt²
d²x/dt² + (k/m).x = 0
x(t) = A.cos(t.V(k/m)) + B.sin(t.V(k/m))
x(0) = Xo --> A = Xo
x(t) = Xo.cos(t.V(k/m)) + B.sin(t.V(k/m))
dx/dt = -Xo.V(k/m) . sin(t.V(k/m)) + B.V(k/m) . cos(t.V(k/m))
Vo = 0 --> (dx/dt)(0) = 0 ---> B = 0
x(t) = Xo.cos(t.V(k/m))
w = V(k/m) = 2Pi/To
To = 2Pi.V(m/k)
c est bon

 (LC)
(LC)

