Inscription / Connexion Nouveau Sujet
Équilibre de trois masses (mécanique)
Bonjour,
J'ai à nouveau un exercice de mécanique niveau approfondi sur lequel j'aurais vraiment besoin d'aide.
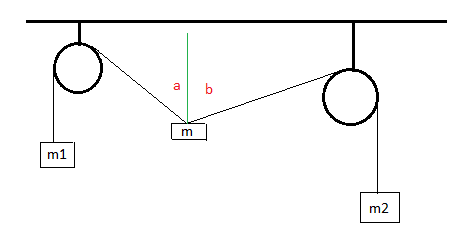
Une masse m est soutenue par deux cordes. Ces cordes partent de m, et passent par deux poulies A et B situées au même niveau par rapport à l'horizontale. A l'autre extrémité de ces cordes, on attache respectivement une masse m1 et m2. Ces deux dernières masses se trouvent à la verticale sous les points A et B. Le point m n'est pas nécessairement équidistant de A et de B. L'ensemble est statique.
1. Trouver les équations permettant de déterminer les angles  1 et
1 et  2.
2.
2. A quelle condition m est-elle équidistante de A et de B ?
3. On choisit m1=m2=1kg. Que se passe t-il si m=3kg.
4. Montrer plus généralement que m est nécessairement bornée par m1+m2 dans le cas statique.
Voilà je commence déjà à bloquer sur la première question. J'essaye de joindre un schéma.
Bonne soirée et merci à ceux qui voudraient bien m'aider.
Bonjour,
Sur ton dessin les poulies ne sont pas vraiment au même niveau par rapport à l'horizontale (cette condition sera nécessaire pour la réponse à la deuxième question).
Quelles sont les forces appliquées au solide de masse m ?
Comment écris-tu l'équilibre statique de ces forces ?

Bonjour Coll,
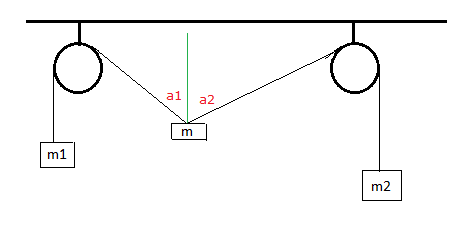
Oui mon dessin ne va pas vraiment... Je l'ai refait : pas très propre mais un peu plus cohérent avec l'énoncé ! (en fin de message). Les angles à déterminer sont en rouge (appelés a1 et a2).
Alors voici ce que j'ai fait pour la question 1...
Bilan des forces de chaque masse :
Pour m1 on a le poids P1 et la tension de la corde T1. Pour m2 on a P2 et T2. Et pour m on a son poids P et les tensions T'1 du côté de l'angle a1 et T'2 du côté de l'angle a2.
En projetant les vecteurs sur le dessin, on peut noter que T1x=T1.sin(a1) et T1y=T1.cos(a1). Et T2x=T2.sin(a2) et T2y=T2.cos(a2).
Ensuite, la condition d'équilibre verticale de m implique T1.sin(a1)+T2sin(a2)=P. Est-ce juste ?
Par contre après je ne vois pas comment déterminer les angles...
Quelle est la direction de l'axe Ox et celle de l'axe Oy ?
Je pose cette question car je ne suis pas d'accord avec ta condition d'équilibre vertical.
__________
Le solide de masse m étant soumis aux trois forces ,
et
la condition d'équilibre s'écrit :

J'ai essayé de tracer mes axes x et y sur le dessin, j'ai pris comme origine la masse m.
Pour les conditions d'équilibre verticales de m, on a la tension T=T'1+T'2 dirigé vers le haut (suivant l'axe y) et le poids P dans le sens contraire à T. Donc T=-P...
D'accord.
Mais tu as écrit :
T1.sin(a1)+T2sin(a2)=P.
et je ne suis pas d'accord avec cela.

En fait je voulais mettre T1y+T2y=-P donc T1cos(a1)+T2cos(a2)=-P...
Voilà comment j'ai représenté les forces T1 et T2...
Oui... "En fait" tu t'étais donc trompé(e)...
Alors comment projeter la condition d'équilibre, qui est une condition vectorielle, pour trouver les équations qui permettent de déterminer les angles ?

Oui j'ai voulu aller trop vite...
Il faudrait ensuite trouver les conditions d'équilibre horizontales ?
On a bien T1x = -T2x soit T1.sin(a1) = - T2.sin(a2) ?
Pour ne pas entrer dans des considérations sans fin sur les signes, je te propose :
m1.sin( 1) = m2.sin(
1) = m2.sin( 2)
2)
En voici une.
Et l'autre :
m = m1.cos( 1) + m2.cos(
1) + m2.cos( 2)
2)
Tu peux maintenant répondre à la deuxième question.
Merci pour ta réponse !
Pour que m soit équidistante de A et B, il faudrait que les angles a1 et a2 soient égaux, c'est bien ça ?
C'est exact !
Quelle est la conséquence sur les valeurs de m1 et m2 ?
Rappel : m1.sin( 1) = m2.sin(
1) = m2.sin( 2)
2)

En fait, pour que m soit équidistante de A et de B, m1 et m2 doivent avoir la même masse, ce qui engendrera les deux angles a1 et a2 égaux ? 
m1=m2=1kg implique que a1 et a2 soient égaux, donc déjà on sait que m sera équidistante de A et de B !
Ainsi :
m = m1.cos(a1)+m2.cos(a2)
3 kg = 1 kg.cos(a1) + 1 kg.cos(a2) (avec a1=a2)
Ce qui fait que le poids de m va l'"emporter" en bas verticalement (vers le sol), puis il va "emporter" m1 et m2 vers le haut (à la verticale), proches des poulies respectives A et B... Je ne sais pas si je suis claire...