Inscription / Connexion Nouveau Sujet
Équations horaires et cartésiennes.
Bonsoir ,
Merci d'avance. 
Un projectile dans le champ de pesanteur avec une vitesse , de direction inclinée d'un angle
avec l'horizontal.
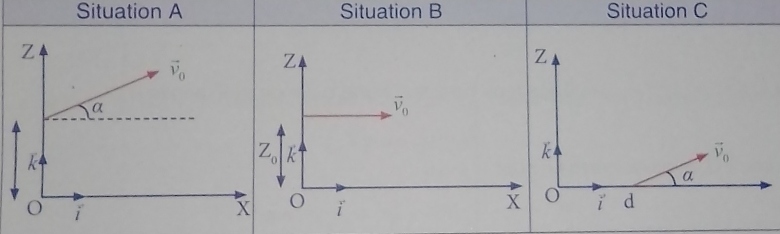
L'étude du mouvement d'un projectile s'effectue dans le repère représenté ci après dans trois situations A , B et C.
Établir pour chaque situation :
1) Les équations horaires du mouvement du projectile ;
2) L'équation cartésienne de la trajectoire.
Réponses
Système : le projectile
Référentiel : Terrestre supposé galiléen.
Bilan des forces : Le poids du projectile.
D'après le théorème de l'énergie cinétique :
(cste : constante).
et
ont la même direction et le même sens.
Le mouvement est uniquement varié.
Le vecteur vitesse du projectile est donc :
Le vecteur position :
Situation 1
À t = 0s , dans le repère (O ; i ; j ;k) ,
À t ≠ 0 s ,
==>
Mais je ne vois pas comment faire pour les deux autres cas..
Bonjour,
Situation 1:
La marche est bonne mais tu as fait des erreurs :
b) L'énoncé impose un repère à deux dimensions, or tu as utilisé un repère à trois dimensions.
b) Tu annonces l'emploi du théorème de l'énergie cinétique, mais tu utilises en fait la deuxième loi de Newton.
c) Ton vecteur est faux : A la date t=0 le projectile n'est pas en O


