Inscription / Connexion Nouveau Sujet
Équation horaire MRUA
Bonjour, voici mon énonce.
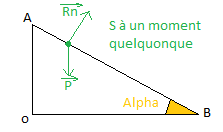
On étudie le mouvement rectiligne uniformément accélèré d'un wagonnet considèré comme un point matériel. Ce dernier a une masse m=195kg
Le wagonnet passe au point A, à t=0 à x(a)=0, a la vitesse Va=1 m.s-1et glisse sans frottements jusqu'au point B. L'angle formé par la piste avec l'horizontale est alpha=53 degrés. La hauteur du point A est z(a)= 8 et celle du point B est z(b)=0
En déduire la valeur de la vitesse v(b) au point B.
Voici ma réponse :
Référentiel terrestre; système S (wagon, rails)
Équation horaire:
a(t)=a
v(t)=at+vo
x(t)=(1/2)a.t2+v0t+z(t)
Si on considère que le wagon est au point b:
x(b)=OB=OA/tan(alpha)
x(b)=8/tan(53)
x(b)=6m
x(b)=(1/2).a.t2+vo.t+0
(On effectue une équation du second degré et on trouve
t=1,37s
Sachant que v(t)=a.t+vo
Alors v(1,37)=7,8x1,37+1
v(1,37)=11,7 m.s-1
...
Mon livre trouve comme réponse v=12,7m.s-1
Je refais les calculs dans tout les sens mais jamais je retombe sur le bon résultats.
Pouvez m'aider?
Bonjour,
Les rails, immobiles, ne font certainement pas partie du système étudié.
Quel est ton repère ? Quels sont tes axes ? Où se trouve le point O ?
As-tu écrit le principe fondamental de la dynamique qui est une relation vectorielle ? Comment projettes-tu cette relation sur les axes ?
__________
Pour ma part, je trouve qu'une résolution en utilisant le théorème de l'énergie cinétique est beaucoup plus simple et rapide. Elle conduit d'ailleurs au résultat annoncé par ton livre...

Bonsoir Coll
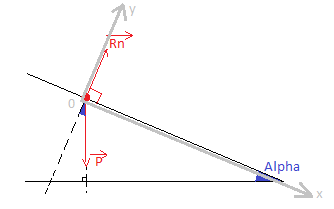
Mon repère est orthonormé (o;i;j)
Le principe fondamentale de la dynamique corresponds à la seconde loi de newton  Forces ext = m.a
Forces ext = m.a
je sais bien qu'on peut y répondre aussi de cette façon mais j'aimerais comprendre mon erreur par la méthode précédente svp
Re bonjour, je reprends mon exercice en corrigeant les erreurs que j'ai trouvé :
Référentiel : Terrestre supposé galiléen Système : (le wagon)
(Voir le schéma)
Equations horaires :
a(x)=a
v(x)= at+v0
x=(1/2)a.t²+v0.t+x0
Il faut d'abord que je détermine la valeur de x lorsque le wagon a terminé sa course donc au bout de AB.
Sin(alpha)= AC/AB AB= AC/sin(alpha) AB= 8/sin(53) ========= > AB=10m
Si je reprends la dernière ligne de mon équation horaire nous avons : x=(1/2)a.t²+v0.t+x0
10 = 3,9 t² +1t +0 === > 3,9 t² +1t -10 = 0
Equation du second degré :
Delta : 1 - 4(3,9 x -10) delta = 157 delta > 0 donc deux solutions (je ne détaille pas tout les calcules ici) :
S1= (1-12,5)/7,8 S1= -1,47 S1< 0 donc S1 impossible
S2= (1+12,5)/7,8 S2= 1,73 (ce résultat est il juste ? mon livre indique S2= 1,55 … bizarre)
T=1,73 s
On reprend donc notre équation horaire de la vitesse :
V(1,73)= 7,8 x 1,73 + 1
V(1 ,73)= 14,5 m.s-1
Alors que mon livre m'indique toujours v(fin)= 12,7 m.s-1
Où est mon erreur ?
Théorème de l'énergie cinétique :
(1/2).m.(vB2 - vA2) = m.g.h
vB2 = vA2 + 2.g.h
Application numérique :
vB 
 (1 + 2
(1 + 2  9,8
9,8  8)
8)  12,6 m.s-1
12,6 m.s-1
___________
Ta méthode :
J'utilise comme repère :
Origine : le point A
Axe des abscisses: AB, orienté de A vers B
Axe des ordonnées : perpendiculaire au précédent
On a un triangle rectangle "3 ; 4 ; 5" à ceci près qu'il est "6 ; 8 ; 10"
AB = 10 m
(tu peux aussi employer la trigonométrie AB = AO / sin( ) = 8 / sin(53°)
) = 8 / sin(53°)  10 m)
10 m)
Durée pour aller de A à B  1,476 s
1,476 s
Vitesse en B : vB  [9,8
[9,8  sin(
sin( )]
)]  1,476 + 1
1,476 + 1  12,6 m.s-1
12,6 m.s-1

Durée pour aller de A à B 1,476 s
J'aimerais juste savoir comment vous avez trouvé ce temps, pouvez vous reprendre mon équation du second degré je dois avoir fais une erreur a ce stade je pense pour le détermination du temps

Équation du second degré...
discriminant :
Il y a deux racines distinctes et
si
Ces racines sont alors
et
_____________
Ici :
et
Physiquement, cette seconde racine correspondrait à un mobile qui remonte de B vers A, dépasse légèrement A avant de redescendre. Ce n'est donc pas la situation physique étudiée.
_____________
Je te laisse comparer ta méthode à l'emploi du théorème de l'énergie cinétique : temps mis pour la résolution, risques d'erreurs de calcul...