Inscription / Connexion Nouveau Sujet
Equation du mouvement
Bonjour à tous,
Alors j'ai un petit problème concernant la question 1 de l'exercice suivant :
relais 4 x 400
Un coureur X arrive avec un mouvement uniforme v=7,5 ms-1. A 10 m devant lui, le coureur Y s'élance d'un mouvement uniformèment accéléré a=2 ms-2.
1.Quel temps s'écoule entre le moment où Y démarre et le passage du témoin.
2.Pendant cette durée quelles sont les distances parcourues par X et Y.
Tous les coureurs ont une accélération de 2 ms-2 jusqu'à atteindre une vitesse v= 7,5 ms-1 qu'il conserve jusqu'au passage du témoin. Les passages du témoin se font tous les 400 m. Quelle est la durée de la course ?
La correction de la question 1 est donnée telle quelle:
origine des temps: t=0 au démarrage de Y
origine des abscisses: position de Y à t=0
équations horaires:
coureur X: x=7,5t-10 coureur Y: x=t² tant que la vitesse est inférieure à 7,5 ms-2.
passage du témoin : les deux coureurs se rejoignent
7,5t-10 = t²
la résolution donne t=1,73 s
la seconde solution t=5,77 s :si X continue à courir à la même vitesse , il va rattraper Y
Le problème est que lorsque que j'intègre la vitesse du coureur X, je trouve ceci :
x-(-10)=vt-(v.(-10/v))
=> x=vt
Je comprend bien qu'il faut signifier que le coureur ne part pas à l'origine des temps, mais comment le retrouver par le calcul d'intégrales ?
Merci par avance à ceux qui me répondront !
Bonjour,
J'avoue ne pas comprendre ta question. Mais tu vas me l'expliquer.
Conditions initiales pour X :
a = 0 (sa vitesse est uniforme)
v = 7,5 m.s-1
x = - 10 m pour l'origine des temps
D'où l'équation horaire de X :
x(t) = 7,5 t - 10
Conditions initiales pour Y :
a = 2 m.s-2
v = 0 m.s-1
x = 0 m
D'où l'équation horaire de Y :
x(t) = (1/2).a.t2 = (1/2) 2
2 t2 = t2
t2 = t2
Ceci pour t  0 s et aussi longtemps que v
0 s et aussi longtemps que v  7,5 m.s-1
7,5 m.s-1
X s'arrête après avoir passé le relais.
À cet instant sa vitesse était supérieure à celle de Y
Si X continuait à courir et si Y continuait à accélérer au-delà d'une vitesse de 7,5 m.s-1 alors Y rattraperait X : d'où la seconde solution de l'équation.
Mais il faut noter que si X continuait à courir à 7,5 m.s-1 et que Y n'accélérait pas au-delà de cette vitesse, Y ne rattraperait pas X qui conserverait la même avance sur lui.
Peux-tu reposer ta question (si tu as toujours une question...) ?

Lorsqu'on intègre ... il y a une constante d'intégration qu'on ne doit pas oublier. Cette constante est déterminée par la ou les conditions initiales.
V = 7,5
V = dx/dt = 7,5
dx/dt = 7,5
dx = 7,5 dt
x(t) = S 7,5 dt (avec S pour le signe intégrale).
x(t) = 7,5.t + K (K est la constante d'intégration)
Comme en t = 0, le coureur X est à l'abscisse -10 (m), on a la condition initiale x(0) = -10
Cette condition permet de calculer la valeur de K :
X(0) = -10
-10 = 7,5*0 + K
K = -10
Et donc finalement : x(t) = 7,5.t - 10 (pour le coureur X)
-----
Sauf distraction. 
Une image à méditer :
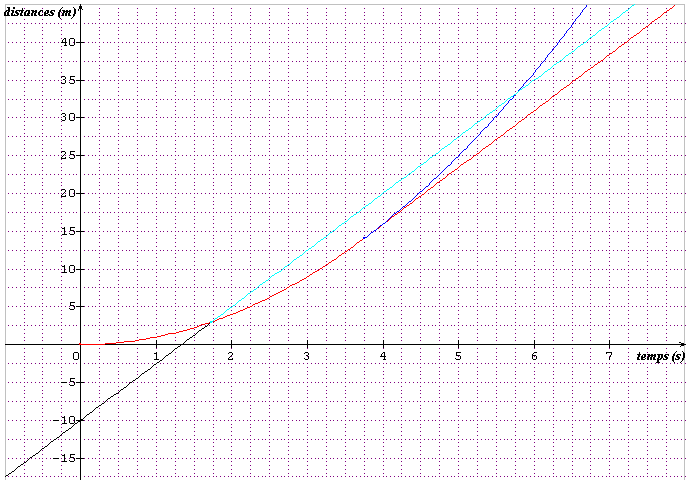
En noir : ce que fait le coureur X jusqu'au passage du relais
En bleu clair : ce qu'il ferait s'il continuait à courir
En rouge : ce que fait le coureur Y
En bleu foncé : ce que ferait le coureur Y s'il continuait d'accélérer au-delà d'une vitesse de 7,5 m.s-1
Tu peux voir la deuxième solution (à 5,77 s) mais elle ne repose pas sur les hypothèses de l'énoncé.
Re - bonjour J-P 

Aaah la constante ... ben c'est plus clair maintenant !
Merci mille-fois à vous pour vos réponses rapides et efficaces !


