Inscription / Connexion Nouveau Sujet
Electricté, circuit RC, variation courant
Bonjour à tous
J'essais de comprendre par moi-même différentes notions concernant les condensateurs équation différentielles et ça marche à peux près
Juste besoin de quelques lumières svp
Voici mon énoncé :
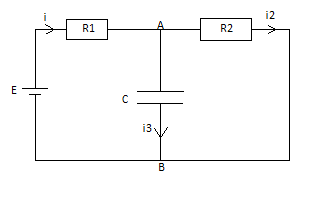
On considère me circuit schématisé sur la figure ci-dessous, dans lequel E représente un générateur idéal de fem : E et de résistance interne nulle. A t=0s, le condensateur est déchargé et on fait fonctionner le générateur.
Répondre par vrai ou faux en justifiant :
A) La tension U(AB) admet comme expression U(AB)= -E+R1i
MA REPONSE : si on considère la boucle de gauche, on applique la loi d'additivité des tensions :
E = U(R1) + U(AB)
E = R1.i + U(AB)
U(AB) = E - R1.i donc FAUX
B) La constante taux a pour expression : taux= ((R1.R2)/(R1+R2)).C
MA REPONSE : la formule générale de taux= R(équivalente) . C
R1 et R2 sont montés en dérivation donc 1/Req = (1/R1) + (1/R2) => Req = ((R1.R2)/(R1+R2))
Jusqu'ici tous vas bien ?
Résultats corrects.
Il faut cependant éviter d'écrire "R1 et R2 sont montés en dérivation", car c'est faux.
R1 et R2 se comportent comme s'ils étaient en dérivarion pour calculer le Req de la constante de temps, cà c'est vrai.
Mais R1 et R2 ne sont pas en dérivation.
Des composants en dérivation ont la même différence de potentiel à leurs bornes ... et ce n'est pas le cas pour R1 et R2.
En fait, R1 et R2 sont "comme si" elles étaient en dérivation du point de vue des de tension puisqu'elles ont une borne commune et que leurs autres bornes sont séparées par une différence de potentiel continue constante (égale à E).

ok bon c'était ce qui me posait le moins problème 
Mon réel problème se trouve ici :
C) La loi donnant i2(t) dans R2 en fonction du temps s'écrit i2(t) = ((E/(R1+R2))e(-t/taux)
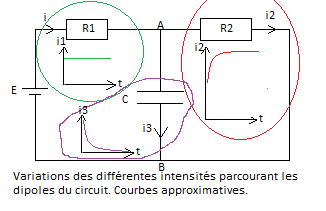
J'essais de comprendre le comportement de l'intensité dans un circuit comme celui-ci. Si on considère qu'à t=0 le circuit est ouvert et le condensateur est déchargé et qu'on ferme le circuit (voir schéma) alors :
-l'intensité 1 (vert) reste constante car i1= i2 + i3, si i1 ne varie par alors cela veut dire que i2 et i3 varient de façon proportionnelles.
I1= E/R1
-l'intensité 3 (violet) diminue au fur et à mesure que le condensateur se charge.
I3= (E/R3)e(-t/taux)
-l'intensité 2 (rouge) augmente au fur et à mesure que i2 diminue.
I2= (E/Req)(1-e(-t/taux))
Ai-je raison ou tord dans mon raisonnement ? merci d'avance
Ce n'est pas vraiment cela.
E = Uc + R1.i
Uc = R2.i2
i3 = C.dUc/dt
i = i2 + i3
-----
On éliminine i
E = Uc + R1.i2 + R1.i3
Uc = R2.i2
i3 = C.dUc/dt
-----
On élimine Uc
E = R2.i2 + R1.i2 + R1.i3
i3 = C.R2.dI2/dt
-----
On élimine i3
E = R2.i2 + R1.i2 + R1.R2.C.dI2/dt
-----
dI2/dt + (R1+R2)/(R1R2C).I2 = E/(R1R2C)
Eq différentielle qui résolue donnc :
I2 = K.e^(-t.(R1+R2)/(R1R2C)) + E/(R1+R2)
Et comme I2(0) = 0 ---> K = -E/(R1+R2)
I2 = E/(R1+R2) * (1 - e^(-t.(R1+R2)/(R1R2C)))
qui n'est pas la même chose que I2= (E/Req)(1-e(-t/taux)) que tu as écrit.
-----
Sauf distraction. 
Oui ok j le suis trompe au niveau de Req différent de R1+R2
Et sinon au niveau de mon schéma hasardeux? L'évolution réel des intensités est bien de ma même forme ?
Le courant i (i1) n'est en tout cas pas constant comme dessiné.
Par exemple :
en t = 0 : i = E/R1
Pour t --> +oo, i = E/(R1+R2)
... Et donc i n'est pas constant avec t.