Inscription / Connexion Nouveau Sujet
DYNAMIQUE NEWTONIENNE système poulie plan incliné
Salut tout le monde j'avais un petit problème avec ce exercice , merci de m'y apporter des éclaircissements
EXERCICE:
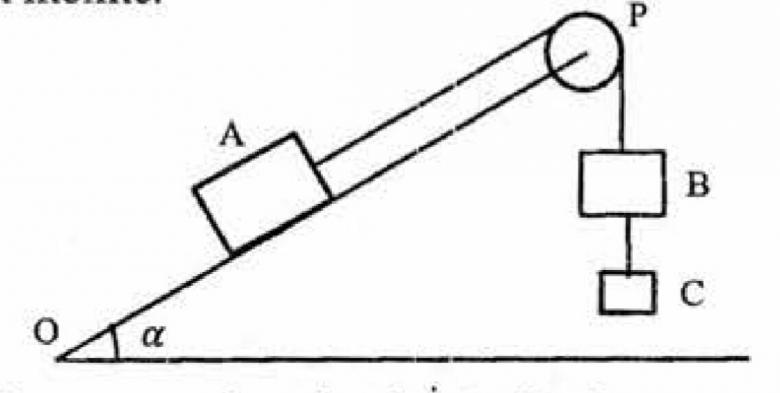
Un corps A de masse m.= 1kg peut glisser sans frottement sur un plan OP incliné d'un angle a== 30° sur le plan horizontal. Ce
corps est attaché par un fil inextensible et de masse négligeable, passant par la gorge d'une poulie d'inertie négligeable, à un
corps B de masse m1 = 400g, auquel est suspendu un autre corps C de masse m2: 200g.
l i Le système est abandonné à lui-même, A se trouve en 0, à la base du plan incline.
al Quelle est l'accélération prise par l'ensemble?
bl Quel est le temps mis par A pour parcourir 1 ,25111?
cl Quelle est la vitesse à cet instant?
dl Quelles sont les tensions des fils liant A à B et B à C? B
21 Après ce parcours de 1 ,25m, C bute sur un obstacle et se décroche.
al Calculer la nouvelle accélération du système.
bl Calculer la distance parcourue par A depuis le départ. c
cl Déterminer la nouvelle tension du fil.
dl Au bout de combien de temps, mesuré depuis le départ de O, A sera-t-il de retour en bas du plan incline?
Calcul de l'accélération de l'ensemble :
On peut :
a) Appliquer et projeter sur un repère qu'on définira avec soin la 2e loi de Newton (RFD) au corps A
b) Faire de même avec l'ensemble {corps B + corps C}
c) En tirer la valeur de l'accélération de l'ensemble compte tenu que (vu les hypothèses simplificatrices de l'énoncé) le module de la tension du fil est constant entre A et B.
Que faire avec le corps B+C , ont ils une relation commune car j'avais déjà fait un exo pareil certes mais sans le corps C
Je ne sais pas ce que tu entends par " relation commune "
D'une manière très générale, pour appliquer correctement la RFD il faut choisir un système.
Le choix de ce système est libre.
Je suggère au paragraphe b) de choisir comme système étudié l'ensemble {corps B + corps C + le fil qui relie B à C } , de rechercher toutes les forces extérieures qui s'exercent dessus et de lui appliquer la RFD qu'on projette ensuite sur un repère adéquat.
Le module de la tension du fil qui relie B avec C est constant.
Rien de nouveau donc avec le module de la tension du fil qui relie A avec B
Par ailleurs si je prenais pas dans le système le fil et que je mette les Tensions T et qur je souhaite appliquer les TEC quelle sera l'expression du travail de la tension des fils WT(vecteur) ?
En langue mathématique :
En langue française :
Le travail de la force sur un déplacement rectiligne AB est égal au produit scalaire des vecteurs
et
lequel est lui même égal au produit du module du vecteur
par le module du vecteur
par le cosinus de l'angle formé par les vecteurs
et
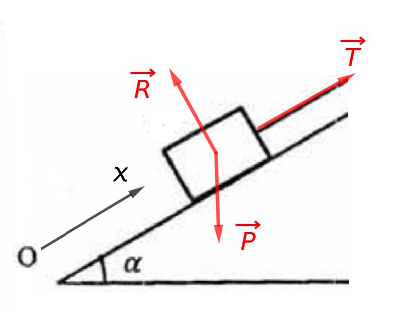
A)système :{A}
Ref.terr.supp.gal.
Bf ,R,T
,R,T
Rfd: -mgsin+T+R=ma
B)système:{B+C}
Rtsg
Bf 1,T1(entre la poulie et B),P2,T2(de B vers C),T2'(de C vers B) or T2+T2'=0(vecteur nul ) car elles sont opposées d'où T2+T2' n'apparaîtra pas dans la RFD
1,T1(entre la poulie et B),P2,T2(de B vers C),T2'(de C vers B) or T2+T2'=0(vecteur nul ) car elles sont opposées d'où T2+T2' n'apparaîtra pas dans la RFD
rfd:T1+P1+P2=(m1+m2)a (le tout en vecteurs)
Correct ?
Désolé, je n'ai pas le courage d'essayer de démêler ton texte bien peu lisible.
Je corrige sommairement l'étude du système A
Projection sur l'axe Ox :
-mg sin( ) + T + 0 = ma
) + T + 0 = ma
soit T = m(a+g sin( )) Relation 1
)) Relation 1
3 forces extérieures seulement s'exercent sur le système {A + B}
Je te laisse faire le même travail que celui que j'ai fait pour le système A
Par projection sur l'axe Oy tu obtiendras la relation 2
En éliminant T des relations 1 et 2 tu exprimeras l'accélération en fonction de m, m1, m2, g et  ce qui te permettras d'obtenir sa valeur numérique.
ce qui te permettras d'obtenir sa valeur numérique.
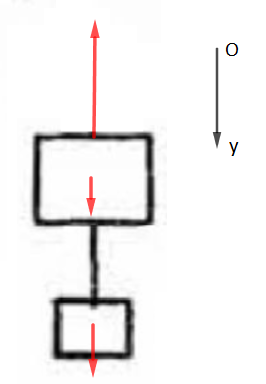
Pour le système B+C
rfd : m1g+m2g-T'=ma ==> T'=(m1+m2)(g-a)
Or le fil est inextensible alors T=T'
m(a+gsin ) = (m1+m2)(g-a)
En développant et en regroupant on a
a=(g(m1+m2-msin)/(m+m1+m2)
Avec l'application numérique sachant que dans tous les cas je prend g=9,8m/s² je trouve a=0,61m/s²
b)le temps mis par A pour parcourir 1,25 m
X(t)=0,5at²+Vot+xo or Vo et xo sont nuls alors x(t)=0,30t²
1,25=0,3t² ==> t=2,04s
C) la vitesse à cet instant
V(t)=at+Vo or vo=0 alors v(t)=0,61t en remplaçant t par 2,04 on a V=1,24m/s
D) les Tensions des fils
Liant A à B
T=m(a+gsin)par l'application numérique on a T=5,51N
Liant B à C là je ne sais pas 😐
2/a. la nouvelle accélération du système
Système:{fils A,B} , (on m'a dit que si je prenais les fils dans le système les Tensions seront des forces interieures , est-ce vrai ? )
Référentiel terrestre
BF: P, R,P1
Tec: 0,5V²(m+m1)=Wp+Wr+Wp1 or Wr=0 alors
0,5V²(m+m1)= x(-mgsin+m1g)
En derivant les deux membres j'ai (m+m1)Va=V(-mgsin +m1g) les V se simplifient puis en divisant par le membre de gauche j'ai
a=(g(-msin+m1)/(m+m1), l'application numérique me donne a=-0,7m/s²
Calculer la distance parcourue par A depuis le départ. je ne sais pas également
La nouvelle tension du fil
Système:{A}
Ref. Terr.
Bf: P,R,T
RFD: P+R+T=ma après projection T=m(a+gsin) mon application numérique me donne T=4,2N
Au bout de combien de temps, mesuré depuis le départ de O, A sera-t-il de retour en bas du plan incline? je ne sais pas
Dans un premier temps je réponds seulement à tes posts du 11-10-18 à 07:06 et 11-10-18 à 07:11
Le reste viendra plus tard.
Pour la Rfd appliquée au système {b+c} l'accélération c'est (m1+m2)a ou bien ??
Cette question n'a aucun sens car une accélération ne peut pas " être " une masse !
Et pourquoi les Tensions T2 de B vers C et T2' de C vers B ne sont pas des forces extérieurs ?
Pour distinguer les forces intérieures des forces extérieures il est indispensable d'avoir défini avec précision le système étudié et bien entendu de connaître les définitions de ces deux types de forces.
Si le fil qui lie B et C fait partie du système étudié, alors les forces exercées par ce fil sont des forces intérieures qui n'ont pas à être prises en compte. C'est une conséquence de la 3ème loi de Newton ( loi des actions réciproques ou loi de l'action et de la réaction ).
Lire ici
Les démarches et les résultats littéraux des parties que tu as développées sont exactes.
Je n'ai pas vérifié les applications numériques.
A ce sujet et sauf indication contraire de l'énoncé (ou du professeur) je conseille de prendre g=10m/s² car on aboutit à des valeurs numériques plus "rondes".
En effet on a souvent la très mauvaise habitude d'utiliser des valeurs arrondies pour poursuivre les calculs ce qui conduit à propager des erreurs d'arrondis et d'aboutir parfois à des résultats faux.
Tension du fil entre B et C :
Définir un nouveau système dans lequel la tension de ce fil est une force extérieure puis utilisr la RFD
Remarque pour la question 2a)
Ta démonstration est exacte mais il aurait été plus simple de faire remarquer que le problème était identique à celui traité à la toute première question à condition d'attribuer à m2 une valeur nulle.
Le résultat est alors immédiat :
A la première question on avait
qui devient donc :
Question 2.a)
Calculer la distance parcourue par A depuis le départ.
Question mal foutue ! on dit " depuis le départ " mais on ne fixe pas quel point d'arrivée doit être pris en considération.
Pour les distances et les durées liées au mouvement de A :
Phase 1 : A part du repos et parcourt une distance OB = 1,25m avec une accélération " a " Il arrive en B avec une vitesse V
Phase 2 : A part de B avec la vitesse V. Son accélération est maintenant " a' "
a' étant négatif, A va ralentir, s'arrêter et redescendre jusqu'à repasser par son point de départ.
Les deux phases obéissent aux lois du mouvement rectiligne uniformément varié.
Tension liant B à C
Système : C
Ref terr
Bf P2 , T2
rfd: P2+T2=m2a ==> m2g-T2=m2a ==> T2=m2(g-a)
Phase 2 l'origine dees dates c 'est 2,04 et à cette date Vo=1,24m/s
X(t)=0,5a't²+1,24t puis ??
Tension T2 : C'est OK
------------------------------------------------------------------------------------
Dire " l'origine des dates c 'est 2,04 " ( surtout sans unité ! ) n'a strictement aucun sens.
Une origine des dates se définit TOUJOURS par le début de phrase :
On prend comme origine des dates l'instant où ..... etc
De même ( et à condition d'avoir défini un repère ce que tu ne fais jamais ) on définit TOUJOURS une origine des espaces par le début de phrase :
On prend comme origine des espaces l'endroit où ..... etc
Ici, tu as implicitement choisi comme repère ( ne pas confondre un repère avec un référentiel ) un axe parallèle à la pente du plan incliné et orienté vers le haut.
Sur ce repère tu as implicitement choisi comme origine des espaces l'endroit ou se trouve A au moment ou C se décroche.
Toujours implicitement tu as choisi comme origine des dates l'instant où C se décroche.
Ton professeur qui, dis tu par ailleurs, est exigeant appréciera que tu fasses des choix explicites et correctement exprimés.
Alors avec ce repère et avec ces origines des espaces et des dates tu peux en effet écrire que :
X(t) = (1/2) a't² + V0t
Et puis ? demande tu
Et bien en dérivant tu obtiendras l'expression de la vitesse de A
V(t) ) = a't + V0
Tu pourras donc en déduire à quelle date θ le mobile A s'arrête.
θ = - V0 / a'
et donc connaître la durée T = θ - 0 = θ de la phase décélérée.
etc .....
Attention en faisant les applications numériques de ne pas utiliser dans les calculs des valeurs approchées comme 1,24 m/s