Inscription / Connexion Nouveau Sujet
Dynamique du point.
Bonjour
Un skieur descend une pente faisant un angle 
avec l'horizontal. Il n'a pas de vitesse initiale. Il commence à une hauteur h.
Tout d'abord on néglige les frottements.
Je trouve :
a*g = P + R
Je projette :
x''(t) = Rx / m
y''(t) = 0
z''(t) = -g + Rz / m
x'(t) = (Rx / m) * t
y'(t) = 0
z'(t) = (-g + Rz / m) * t
x(t) = 1/2 * (Rx / m) * t²
y(t) = 0
z(t) = 1/2 * (-g + Rz / m) * t²
Comment continuer afin de trouver la durée de la descente? Comment trouver les composantes de R ? Merci.
bonsoir,
si l'énoncé ne précise par le repère à prendre pour faire l'étude,
je te conseille le repère Oxy indiqué ci-dessous:
avec M en O à t=0
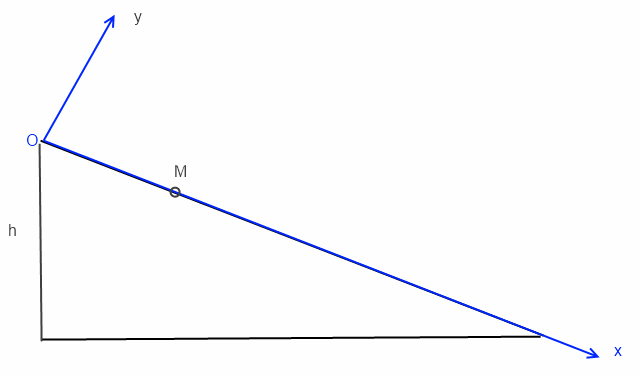
En prenant ton repère je trouve :
x''(t) = sin * m * g
y''(t) = -cos * m * g + Rz
Que faire ensuite?
oui avec y= 0 = cste donc y' = y" =0
ce qui te donne la réaction normale Ry
l'autre équation te donne x(t)
En fait j'avais fait une erreur. Je reprends :
x''(t) = sin * g
y''(t) = -cos * g + Ry/m
Comme y''(t) = 0, on a :
Ry = cos * g * m
Finalement :
x(t) = 1/2 (sin * g)* t²
y(t) = 0
Pour calculer le temps que le skieur met à descendre :
x(t) = h/sin
1/2 sin * g * t² = h/sin
t = 
(2h / (sin²*g))
Est-ce correct?
Annuler
connectez vous