Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Niveau terminale
Partager :

Dynamique de rotation 2

Posté par
hdiallo 13-05-23 à 16:33

Bonjour, je sollicite votre aide.

Problème
On considère le dispositif ci-dessous :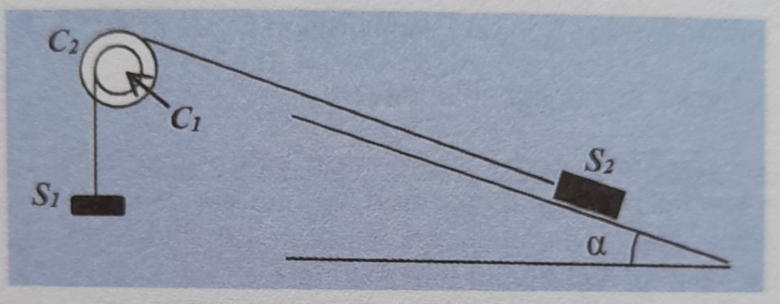Dynamique de rotation 2 (C1) et (C2) sont deux cylindres homogènes de même axe de révolution (), de masses respectives m1 et m2 et de rayons respectifs R1 et R2.
AB est un plan incliné de = 30⁰ par rapport au plan horizontal. (S1) et (S2) sont des solides supposés ponctuels de masses respectives M1 et M2. Ondonne : R2 = 2R1 = 20 cm ; m2 = 4m1 = 800 g ; M1 = 5M2 = 1 kg.
Le système est abandonné sans vitesse.
1) Dans quel sens les cylindres vont-ils tourner ? Justifier votre réponse.
2) Calculer :
a) l'accélération angulaire des poulies ;
b) l'accélération linéaire de chacun des solides S1 et S2.
3) Calculer la tension de chaque brin de fil.
4) Calculer la variation de l'énergie cinétique du système entre l'instant de départ et l'instant où la vitesse de (S1) atteint la valeur V1 = 1 m/s.
Vérifier le théorème de l'énergie cinétique.
5) A l'instant où la vitesse de (S1) devient égale à 1 m/s, le fil maintenant (S2) se casse en déclenchant un dispositif qui freine le système en exerçant sur les cylindres un couple de forces de moment constant.
Calculer sachant que le système s'immobilise 10 s après la rupture du fil.

Posté par
vanoisere : Dynamique de rotation 2 13-05-23 à 16:39

Bonjour
Pour répondre à la question 1 sans avoir traité la question 2, on peut comparer les moments des deux tensions des deux fils par rapport à l'axe dans le cadre de la statique.

Posté par
hdiallore : Dynamique de rotation 2 13-05-23 à 19:21

Comment cela serait-il possible, alors que les tensions sont inconnues, les moments également ?

Posté par
vanoisere : Dynamique de rotation 2 13-05-23 à 21:44

C'est extrêmement simple en statique.

Posté par
hdiallore : Dynamique de rotation 2 13-05-23 à 22:33

Je me demande si on ne pouvait pas raisonner directement sur les masses en disant ceci :
Puisque M1 est 5 fois plus que M2, donc le système la masse M1 entraîne la masse M2.

Le raisonnement dans le cadre statique, j'avoue que je n'ai compris comment débuter. Ça me gêne beaucoup !

Posté par
vanoisere : Dynamique de rotation 2 13-05-23 à 22:43

En statique, la somme des forces appliquées sur chacune des masses est de résultante nulle. La force exercée par le fil n° 1 sur C1 est tout simplement égale au poids de M1. La force exercée par le fil n° 2 sur C2 est la composante du poids de M1 suivant un axe colinéaire à la ligne de plus grande pente du plan incliné. Reste alors à comparer les moments par rapport à l'axe de rotation de ces deux forces exercées par les deux fils sur le solide mobile autour de cet axe. Cela doit se justifier proprement tout de même !

Posté par
hdiallore : Dynamique de rotation 2 16-05-23 à 01:22

Question 1 : sens du mouvement
Soit le schéma ci-dessous 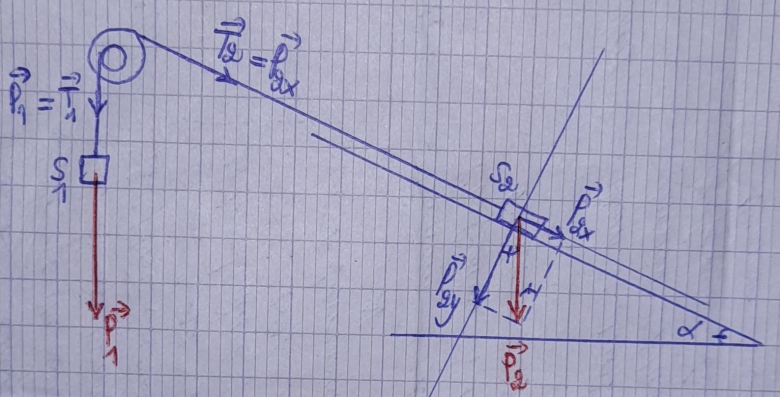Dynamique de rotation 2
J'ai calculé les moments des tensions des deux brins de fil, j'ai évalué leur rapport et j'ai obtenu ceci : (T1) = 5smb]mu[/smb](T2)

Posté par
vanoisere : Dynamique de rotation 2 16-05-23 à 13:43

Ne pas oublier la réaction du plan incliné sur S2 et l'action de l'axe sur le solide constitué des deux cylindres qui les empêchent de tomber. Mais cela ne change pas les calculs. D'accord avec ton résultat. D'où la réponse à la question 1 ?

Posté par
hdiallore : Dynamique de rotation 2 16-05-23 à 14:03

Donc les cylindres vont tourner dans le sens de S1

Posté par
vanoisere : Dynamique de rotation 2 16-05-23 à 15:14

Disons que S1 va descendre et donc S2 monter le long du plan incliné. Compte tenu de cela, tu as intérêt à orienter les axes de façon à obtenir vitesse et accélération positives.

Posté par
hdiallore : Dynamique de rotation 2 28-05-23 à 12:37

D'accord.

Question 2.a) : On demande de Calculer l'accélération angulaire des poulies.

Avant de commencer, j'aimerais savoir si les deux poulies (Rayons différents) ont même accélération angulaire.

Posté par
vanoisere : Dynamique de rotation 2 28-05-23 à 13:38

Oui. Sachant que les fils ne glissement pas sur les poulies, tu va trouver une relation simple entre l'accélération angulaire du solide en rotation, les accélérations des deux masses, R1 et R2.

Posté par
hdiallore : Dynamique de rotation 2 28-05-23 à 16:14

Maintenant, je peux utiliser le Théorème de l'accélération angulaire sur chaque poulie. Ici, si je comprend bien, les tensions des brins de fil de part et d'autre des deux poulies sont différentes.

• sur la grande poulie de rayon R2 :
\mu _ {\vec T_2} = T_2.R_2 = m_2.\alpha''


• sur la petite poulie de rayon R1 :
\mu _ {\vec T_1} = T_1.R_1 = m_1.\alpha''

vanoise, je n'ai pas compris comment faire pour répondre à cette question, honnêtement.

Posté par
vanoisere : Dynamique de rotation 2 28-05-23 à 18:09

Argument déjà utilisé dans un autre problème : les fils ne glissent pas sur les poulies. La vitesse linéaire d'un fil est aussi sa vitesse de rotation quand il est en contact avec la poulie :

\begin{cases} \\ v_{1}=R_{1}.\dot{\alpha}\\ \\ v_{2}=R_{2}.\dot{\alpha} \\ \end{cases}

En dérivant par rapport au temps :

\begin{cases} \\ a_{1}=R_{1}.\ddot{\alpha}\\ \\ a_{2}=R_{2}.\ddot{\alpha} \\ \end{cases}

Posté par
hdiallore : Dynamique de rotation 2 28-05-23 à 19:51

Je ne sais pourquoi je ne trouve pas ces relations assez simple.

En faisant somme membre à membre, J'obtiens

\alpha

Posté par
vanoisere : Dynamique de rotation 2 28-05-23 à 21:06

Tu peux fournir l'expression obtenue de l'accélération angulaire, histoire de poursuivre sur de bonnes bases ?

Posté par
hdiallore : Dynamique de rotation 2 28-05-23 à 21:47

L'accélération angulaire est
'' = (a1 + a2)/(R1 + R2)

Posté par
vanoisere : Dynamique de rotation 2 28-05-23 à 22:18

Je pense à l'expression de l'accélération en fonction des masses et de .

Posté par
hdiallore : Dynamique de rotation 2 28-05-23 à 23:09

Donc, si je comprend bien, je dois appliquer le TCI sur S1 puis sur S2 pour calculer a1 et a2. C'est ça ?

Posté par
hdiallore : Dynamique de rotation 2 29-05-23 à 11:30

vanoise, j'ai repris le schéma.
Sur la figure, d'après le principe des actions réciproques les tensions T2 et T2' sont égales ; de même les tensions T1 et T1' sont aussi égales.
Mais si J'applique le TCI sur S1 j'obtiens a1 = 0 ; de même a2 = 0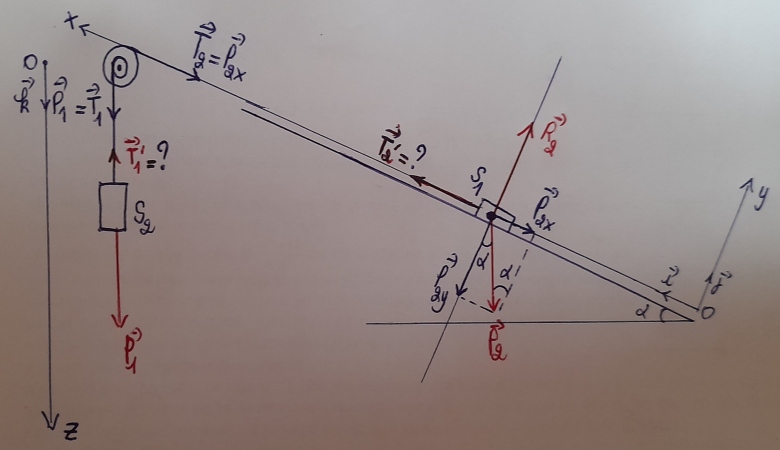Dynamique de rotation 2

Posté par
vanoisere : Dynamique de rotation 2 29-05-23 à 12:41

Tu as permuté S1 et S2 sur le dernier schéma.
Attention : T2=P2x et T1=P1 seulement en statique !Les lois de la dynamique appliquées à S1, S2 puis C, conduisent à :

\begin{cases} \\ M_{1}.a_{1}=M_{1}.g-T'_{1} & (1)\\ \\ M_{2}.a_{2}=T'_{2}-M_{2}.g.\sin\left(\alpha\right) & (2)\\ \\ \frac{1}{2}\left(m_{1}.R_{1}^{2}+m_{2}.R_{2}^{2}\right).\ddot{\alpha}=T_{1}.R_{1}-T_{2}.R_{2} & (3) \\ \end{cases}

Il faut simplifier ces trois équations en tenant compte des deux fils : ils sont de masses négligeables, ils sont inextensibles et ils ne glissent pas sur les poulies.

Une fois cela fait, multiplier (1) par R1, multiplier (2) par R2 puis faire une addition « membre à membre » des trois équations, permet d'éliminer les tensions et d'obtenir l'expression de l'accélération angulaire.

Posté par
hdiallore : Dynamique de rotation 2 29-05-23 à 13:10

Citation :
Il faut simplifier ces trois équations en tenant compte des deux fils : ils sont de masses négligeables, ils sont inextensibles et ils ne glissent pas sur les poulies.

Donc ça veut dire que les tensions de part et d'autre des brins de fil sont égales. C'est ça ?

Posté par
vanoisere : Dynamique de rotation 2 29-05-23 à 14:19

Fils de masses négligeables : la norme de la tension se conserve le long de chaque brin de fil :

T1=T'1 ; T2=T'2.

Fils inextensibles ne glissant pas sur les poulies :

a_{1}=R_{1}.\ddot{\alpha} ; a_{2}=R_{2}.\ddot{\alpha}

En injectant ces égalités dans les trois premières équations :

\begin{cases} \\ M_{1}.R_{1}.\ddot{\alpha}=M_{1}.g-T_{1} & (1)\\ \\ M_{2}.R_{2}.\ddot{\alpha}=T_{2}-M_{2}.g.\sin\left(\alpha\right) & (2)\\ \\ \frac{1}{2}\left(m_{1}.R_{1}^{2}+m_{2}.R_{2}^{2}\right).\ddot{\alpha}=T_{1}.R_{1}-T_{2}.R_{2} & (3) \\ \end{cases}

Méthode décrite dans mon précédent message :

\begin{cases} \\ M_{1}.R_{1}^{2}.\ddot{\alpha}=M_{1}.g.R_{1}-T_{1}.R_{1} & (1)\\ \\ M_{2}.R_{2}^{2}.\ddot{\alpha}=T_{2}.R_{2}-M_{2}.g.R_{2}.\sin\left(\alpha\right) & (2)\\ \\ \frac{1}{2}\left(m_{1}.R_{1}^{2}+m_{2}.R_{2}^{2}\right).\ddot{\alpha}=T_{1}.R_{1}-T_{2}.R_{2} & (3) \\ \end{cases}

Addition « membre à membre »...

Posté par
hdiallore : Dynamique de rotation 2 11-06-23 à 11:11

D'accord !
J'ai fait addition membre à membre. Pour réduire l'expression j'ai tenu compte de la relation entre M1 et M2, m1 et m2, puis R1 et R2.
J'ai trouvé ceci :

\alpha '' = \frac{M_2R_1(5-2sin\alpha)}{9M_2R_1²+\frac{17}{2}m_1R_1²}g

AN : M2 = ⅕ kg = 0,2 kg ; R1 = 0,1 m ; sin = 0,5 ; m1 = 0,4 kg ; je prend g = 9,8 m/s²

Je trouve \alpha '' = 11,2 rad/s²

2.b) On demande l'accélération linéaire de chacun des solides S1 et S2:

On pose a1 = R1" et a2 = R2"

Je fais l'application numérique, je trouve :

a1 = 1,12 m/s²  et a2 = 2,24 m/s²

3) Calculons T1 et T2

A partir des relations de ton post du 29-05-23 à 14:19, on déduit T1 et T2

T1 = M1g - M1R1"
T2 = M2R2" + M2g.sin

AN : T1 = 8,68 N  et  T2 = 1,428 N

Posté par
vanoisere : Dynamique de rotation 2 11-06-23 à 14:18

D'accord avec tes résultats littéraux mais tu écrivais dans ton premier message : m1=0,2kg alors que tu as utilisé : m2=0,4kg ???

Posté par
hdiallore : Dynamique de rotation 2 12-06-23 à 10:05

Ah d'accord, j'ai commis une erreur.
Pour m1 = 0,2 kg Je trouve :

" = 22,4 rad/s² ;
a1 = 2,24 m/s² et a2 = 4,48 m/s² ;
T1 = 7,56 N et T2 = 1,876 N

Posté par
hdiallore : Dynamique de rotation 2 12-06-23 à 10:36

Question 4) : On demande de Calculer la variation de l'énergie cinétique du système au moment où la vitesse de S1 vaut v1 = 1 m/s.

Le système est composé de S1, S2 et les deux poulies.

Puisque les deux brins de fil se trouvent sur deux poulies différentes, v1 est différent de v2.
La variation de l'énergie cinétique du système est :
Ec = Ec - Ec0
Or Ec0 = 0 à l'instant initial.
Donc Ec = Ec
Mais l'énergie cinétique finale du système est la somme des énergies cinétiques de S1, S2 et des deux poulies.
Soient :
• Ec1 = ½mv1² L'énergie cinétique de S1 ;
• Ec2 = ½mv2² L'énergie cinétique de S2 ;
• Ek1 = ½J.1² L'énergie cinétique de la poulie de rayon R1 ;
• Ek2 = ½J.2² L'énergie cinétique de la poulie de rayon R2.

La variation de l'énergie cinétique du système entier est :
Ec = ½m1v1² + ½m2v2² + ½J.1² + ½J.2²

Pour la poulie intérieure J = M1R1² ;
Pour la grande poulie J = M2R2².
De même 1 = v1/R1  et  2 = v2/R2.

Maintenant mon problème, c'est comment chercher v2.

Je ne sais pas si je suis sur le bon chemin

Posté par
vanoisere : Dynamique de rotation 2 12-06-23 à 13:47

Bonne méthode mais attention : les deux poulies forment un même solide de vitesse angulaire :

\omega=\dfrac{v_{1}}{R_{1}}=\dfrac{v_{2}}{R_{2}}

Posté par
hdiallore : Dynamique de rotation 2 12-06-23 à 17:14

Donc Ec = ½m1v1² + ½m2v2² + ½J.²

= v1/R1 = 10 rad/s ;
v2 = R2. = 2 m/s ;
J = J1 + J2 = M1R1² + M2R2² = 9.10-3 kg.m²
C'est ça ?

Posté par
vanoisere : Dynamique de rotation 2 12-06-23 à 18:09

Tu oublies le facteur 1/2 dans l'expression des moments d'inertie des disques supposés homogènes. Le reste est correct.

Posté par
hdiallore : Dynamique de rotation 2 12-06-23 à 20:35

J = J1 + J2 = ½(M1R1² + M2R2²)

J'obtiens J = 4,5.10-3 kg.m²

En remplaçant ces valeurs dans l'expression de la variation de l'énergie cinétique, je trouve :
Ec = 1,925 J

Posté par
hdiallore : Dynamique de rotation 2 13-06-23 à 22:53

Si la variation de l'énergie cinétique que j'ai calculé est correcte, on demande de vérifier le théorème de l'énergie cinétique.
Cela revient donc à calculer la valeur algébrique de la somme des travaux de toutes les forces extérieures pour voir si on aura la valeur de Ec calculée ci-haut.
C'est ça ?

Posté par
vanoisere : Dynamique de rotation 2 14-06-23 à 12:31

Oui. Cela va te ramener à la somme algébrique des travaux des deux poids. A noter que cette méthode aurait permis d'obtenir l'expression de l'accélération mais ce n'est pas la méthode demandée ici.

Posté par
hdiallore : Dynamique de rotation 2 14-06-23 à 20:57

Donc, en prenant comme système (S1 + S2 + Poulies), les tensions des brins de fil sont deviennent des forces intérieures.
Les forces extérieures appliquées au système sont :
- Le poids \vec P_1 de S1 ;
- Le poids \vec P_2 de S2 ;
- la réaction \vec R du plan incliné sur S2 ;
- la réaction \vec R' de l'axe de rotation sur les poulies.
Seuls les poids effectuent des travaux non nuls.
W(\vec P_1) = m_1gx ;
W(\vec P_2) = - m_2gx.sin\alpha
NB : j'ai considéré que si S1 descend d'une hauteur x, S2 parcours la même distance x le long du plan incliné.
C'est ça ?

Posté par
vanoisere : Dynamique de rotation 2 14-06-23 à 21:03

Oui !

Posté par
hdiallore : Dynamique de rotation 2 15-06-23 à 06:29

Petit soucis...
J'ai essayé de déterminer x, je trouve deux valeurs différentes.
Voici ma méthode :
▪︎ sur solide S1, v1² = 2a1x ;
▪︎ surle solide S2, v2² = 2a2.x

Posté par
vanoisere : Dynamique de rotation 2 15-06-23 à 10:10

La relation de mon message du 12-06-23 à 13:47 conduit par intégration par rapport au temps à :

\alpha=\dfrac{x_{1}}{R_{1}}=\dfrac{x_{2}}{R_{2}}

Posté par
hdiallore : Dynamique de rotation 2 16-06-23 à 07:17

Donc x_1 = R_1\alpha  et  x_2 = R_2\alpha
Si je comprend bien, x_1 \neq x_2.
Comment calculer \alpha ?

Posté par
hdiallore : Dynamique de rotation 2 16-06-23 à 10:55

vanoise, je commence à être perdu là.
Moi j'avais cru que si S1 descend d'une distance x, alors S2 parcourt la même distance Sur le plan incliné.
Mais à voir tes relations, x1 est différent de x2.

L'autre analyse que j'ai faites, les accélérations étant différentes ( a_1 \neq a_2 ), les vitesses linéaires différentes (v_1 \neq v_2), alors pendant la même durée c'est normal que S1 et S2 parcourent des distances différentes.

Aidez-moi à bien comprendre svp.

Posté par
vanoisere : Dynamique de rotation 2 16-06-23 à 12:21

Les deux poulies sont solidaires pour former un même solide. En un temps donné, elles tournent donc du même angle mais, comme les rayons sont différents, les longueurs des deux fils qui s'enroule ou se déroule sont différentes : x1x2.
Puisque tu donnais a1 et v1, facile d'obtenir x1. Ensuite, comme déjà écrit :

x_2=\dfrac{R_2}{R_1}\cdot x_1

Posté par
hdiallore : Dynamique de rotation 2 16-06-23 à 14:33

Maintenant j'ai bien compris !
v_1² = 2.a_1.x_1\Rightarrow x_1 = \frac {v_1²}{2a_1}

Or x_2=\dfrac{R_2}{R_1}\cdot x_1

Or R2 = 2R1, et en jouant un peu avec les relations, je trouve x_2 = 2x_1

AN : x_1 =0,223 m  et  x_2=0,446m

Donc \sum{W(\vec F_{ext})} = W(\vec P_1) + W(\vec P_2) = m_1gx_1 - m_2gx_2sin\alpha

AN : \sum{W(\vec F_{ext})} = - 0,448 J

Problème...puisque la somme des travaux des forces ne donne pas la variation de l'énergie cinétique calculée ci-haut.

Posté par
vanoisere : Dynamique de rotation 2 16-06-23 à 15:09

J'aurais dû le faire remarquer plus tôt : les masses des solides en translation sont M1 et M2.

Posté par
hdiallore : Dynamique de rotation 2 16-06-23 à 21:11


Donc \sum{W(\vec F_{ext})} = W(\vec P_1) + W(\vec P_2) = M_1gx_1 - M_2gx_2sin\alpha =1,75 J

Toujours problème...ça ne donne pas 1,925 J

Posté par
vanoisere : Dynamique de rotation 2 16-06-23 à 21:42

La même confusion semble avoir été faite dans le calcul de l'énergie cinétique.

Posté par
hdiallore : Dynamique de rotation 2 16-06-23 à 21:54

Ah oui, ça fonctionne maintenant !
\Delta E_c = \sum{W(\vec F_{ext}) = 1,75 J}

Posté par
hdiallore : Dynamique de rotation 2 16-06-23 à 22:16

À présent la question 5), on demande de Calculer le moment du couple de freinage :

J'applique le Théorème de l'énergie cinétique aux cylindres :

Ec = . ; où est la vitesse angulaire de rotation des cylindres.

Or l'énergie cinétique finale est nulle à l'arrêt. Donc le Théorème cinétique devient -Ec0 =

Mais Ec0 = ½J² et = ½"t² + t
Je ne sais pas si je suis sur la bonne voie...

Posté par
vanoisere : Dynamique de rotation 2 17-06-23 à 18:04

Plus simple :
v1=R1..

Posté par
hdiallore : Dynamique de rotation 2 17-06-23 à 18:35

Oui = 10 rad/s.

Et a1 = R1." = a1/R1

Posté par
vanoisere : Dynamique de rotation 2 18-06-23 à 19:12

Je reprends tes calculs à partir de la variation d'énergie cinétique lorsque la vitesse du solide 1 vaut V1=1m/s; Je n'utilise que des formules déjà écrites et justifiées.

\Delta E_{c}=\frac{1}{2}M_{1}.V_{1}^{2}+\frac{1}{2}M_{2}.V_{2}^{2}+\frac{1}{2}\left(\frac{1}{2}m_{1}.R_{1}^{2}+\frac{1}{2}m_{2}.R_{2}^{2}\right)\omega^{2}

\Delta E_{c}=\frac{1}{2}M_{1}.V_{1}^{2}+\frac{1}{2}M_{2}.\left(\frac{R_{2}.V_{1}}{R_{1}}\right)^{2}+\frac{1}{4}\left(m_{1}.R_{1}^{2}+m_{2}.R_{2}^{2}\right).\left(\frac{V_{1}}{R_{1}}\right)^{2}

Après simplification, l'application numérique conduit à :

\\ \Delta E_{c}=1,75J

Déplacement entre l'instant initial et l'instant correspondant à V1=1m/s :

x_{1}=\frac{V_{1}^{2}}{2a_{1}}

Le travail total entre ces deux instants vaut :

W=M_{1}.g.x_{1}-M_{2}.g.x_{2}.\sin\left(\alpha\right) \\ \\ W=M_{1}.g.x_{1}-M_{2}.g.\frac{R_{2}}{R_{1}}.x_{1}.\sin\left(\alpha\right)

Après simplification, l'application numérique conduit à :

\\ W=1,75J

Posté par
hdiallore : Dynamique de rotation 2 19-06-23 à 01:18

Oui vanoise, je crois que j'ai déjà fait cela.
Maintenant je suis au niveau de la question 5)

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !