Inscription / Connexion Nouveau Sujet
(DM) Oscilloscope - mouvements des électrons
Bonjour !
J'ai deux exercices à faire pour un DM, je viens quémander un peu d'aide pour le second.
Voici l'énoncé (**p.*** - Physique-Chimie Tle S éditions *****) :
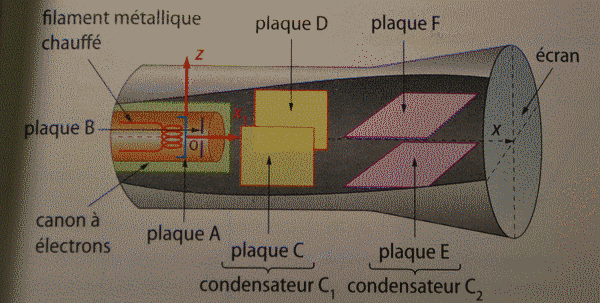
Un oscilloscope comporte un tube cathodique, qui se divise en quatre parties:
- un canon à électrons, où le faisceau d'électrons est créé et les électrons accélérés ;
- un condensateur plan C1 d'armatures verticales, à l'intérieur duquel les électrons sont déviés horizontalement ;
- un condensateur plan C2 d'armatures horizontales, à l'intérieur duquel les électrons sont déviés verticalement ;
- un écran fluorescent, sur lequel l'impact du faisceau laisse une trace lumineuse : le spot.
On étudie le système électron, de charge -e dans le référentiel terrestre supposé galiléen. L'action mécanique de la Terre sur l'électron est négligé.
Donnée: masse de l'électron : m=9,1*10^-31 kg
Les électrons émis ont une vitesse initiale négligeable. Ils sont ensuite accélérés à l'intérieur d'un condensateur plan où règne un champ électrostatique uniforme E1(vecteur). Sa valeur est E1=UAB/dAB avec UAB=-1,8kV et dAB la distance entre les deux armatures.
1) Rappeler les trois caractéristiques du vecteur champ électrostatique à l'intérieur d'un condensateur plan.
- Il "dirige" le vecteur accélération
- Il forme un plan avec le vecteur V0 où le mouvement du centre d'inertie d'une particule s'effectue
- La trajectoire de l'électron dans ce plan est une particule.
2)a- Dans le repère (O ; x1), appliquer la deuxième loi de Newton à l'électron afin de déterminer les expressions de la vitesse v1(t) de l'électron et sa position x1(t) entre les armatures A et B.
b- Déterminer l'expression de la vitesse v1 d'une électron lorsqu'il parvient à la plaque B du condensateur en fonction de e, m, et UAB.
c- Calculer la valeur de cette vitesse en utilisant l'égalité approchée : (V=racine carrée) V6,4 = 2,5.
3) Pour simplifier l'étude, on ne s'intéresse qu'à la déviation du faisceau dans le condensateur C2. Celui-ci est soumis à une tension UFE=U, qui crée un champ électrostatique uniforme E2(vecteur) tel que E2=U/dEF où dEF est la distance entre les deux armatures. On considère que le mouvement de l'électron est plan et s'effectue dans le plan (xOz). Un électron arrive en O avec la vitesse v1 de direction (Ox) à la date t0=0.
Dans ce nouveau repère, etablir, en fonction de E2, m et e, les expressions des coordonnées du vecteur vitesse v2 de l'électron, les expressions des coordonnées du vecteur position à l'intérieur du condensateur C2 et l'équation de la trajectoire.
-----
Comme vous pouvez le voir, je n'ai réussi à répondre qu'à la première question, bloquant complètement sur les autres. Je vous remercie d'avance pour d'éventuels conseils de méthode et autres coups de pouce qui pourraient bien m'aider.
Lylee
Edit Coll
Bonjour
Concernant la première question, je pense que tu ne réponds pas à ce qui est demandé:
Le champ vectoriel est uniforme entre les armatures d'un condensateur plan (même direction, même sens, même intensité), ce qui peut être formulé par 3 caractéristiques:
1) lignes de champ parallèles (perpendiculaires aux armatures)
2) champ dirigé de l'armature portant le grand potentiel vers l'armature portant le plus petit potentiel
3) norme du champ constante
Pour répondre aux questions suivantes:
Le poids étant négligé (cf. énoncé), l'électron est soumis à 2 forces reésultantes des 2 champs électrostatiques et
entre les armatures de C1 et C2
La 2nde loi de Newton te dit par ailleurs que
Donc en projetant cette égalité vectorielle sur les axes de ton repère puis en intégrant successivement pour trouver la vitesse et la position ... tu réponds à la question 2) (en porjetant sur Ox) et 3) en projetant sur Oz).
Est ce plus clair?
PS: quelques résultats de Cours
Bonjour PerArGal,
tout d'abord, merci de ta réponse. Je comprends en effet pour la première question déjà, mes erreurs venant que nous n'avons encore pas le cours sur ce chapitre-ci et que ces caractéristiques ne sont pas énoncées dans mon manuel, à moins que je ne les aies simplement pas trouvées.
En revanche j'ai un peu plus de mal pour l'autre raisonnement, enfin je comprends un peu la méthode, mais je ne sais pas comment dessiner ces forces sur mon repère pour ensuite les projeter, ainsi que l'histoire d'intégrer pour la vitesse et la position.. Oui j'ai beaucoup de mal sur e chapitre ! ;-(
Re-
Revenons alors à la 2eme loi de Newton
Je n'ai pas le schéma du montage mais je suppose que dans un premier temps l'électron est soumis au champ E1 en passant entre les armatures de C1, puis soumis au champ E2 en passant entre les armatures de C2.
Nous nous interessons ici à la 1ere phase:
Dans le repère (xOz) où nou noterons et
les vecteurs unitaires, nous avons
= -e.E1.
Et
donc m.ax = -e.E1
et m.az = 0
(avec bien sûr E1 = UAB / dAB, à la précision du signe près que donne peut être ton schéma)
En supposant que l'électron arrive avec une vitesse négligeable entre les armatures de C1
Et en integrant les 2 équations ci dessus pour trouver la vitesse:
En intégrant une nouvelle fois pour la position:
Voila pour le 2). Enfin sauf erreur d'inattention de ma part. Même raisonnement pour le 3) où la déviation s'poère sur Oz.
Mea Culpa
Dans les expressions de la vitesse et de la position il manque le facteur E1. Ouppsss ...
Il faut donc lire
En espérant que je ne laisse aucune autre coquille.
Et je jette un oeil sur ce que tu proposeras pour la 2nde phase du mouvement
Merci PerArGal,
je crois comprendre le raisonnement du début, mais pas le principe de l'intégration pour la vitesse et la position.. Saurais-tu me l'expliquer, sans trop te prendre la tête évidemment ?
Aïe!!!
Je prends donc comme point de départ les composantes de l'accélération sur les axes Ox et Oz en supposant qu'à ce stade du raisonnement, tout est encore OK pour toi:
On a donc:
Ce qui te dit que l'accélération suivant Ox est constante dans le temps et propotionnelle au champ électroqtatique
et que l'accélération suivant l'axe Oz est nulle
Tu sais:
1) que l'accélération est la dérivée par rapport au temps de la vitesse
2) que la vitesse est la dérivée par rapport au temps de la position
(et que du coup, l'accélération est la dérivée seconde par rapport au temps de la position)
Donc, en "sens inverse":
1) la vitesse est "une primitive" de l'accélération
2) la position est "une primitive" de la vitesse
Pour trouver la vitesse à l'instant t, tu calcules l'intégrale de l'accélération entre l'instant 0 et l'instant t
De même
Pour trouver la position à l'instant t, tu calcules l'intégrale de la vitesse entre l'instant 0 et l'instant t
Comme tu connais le vecteur accélération par ses deux composantes suivant les axes Ox et Oz, tu dois calculer les intégrales de ces composantes pour obtenir les composantes de la vitesse suivant ces deux axes, et donc le vecteur vitesse ...
Détaillons les étapes
(u représentant la variable temps dans l'intervalle [0,t])
On a considéré qu'à t = 0 la vitesse est négligeable, donc v_{x,t=0} = v_{z,t=0} = 0
Et on obtient bien les égaltiés:
Soit, vectoriellement:
Niveau détail des explications je suis à bloc:
1) si tu coinces sur un étape, tu fais signe, on reformulera encore mieux 
2) Pour trouver sa position x_1(t) tu conduis le même raisonnement en intégrant la vitesse cette fois. La encore n'hésite pas à sonner si problème.
Courage! Une fois que tu auras conduis le même raisonnement pour le passage entre les plaques du second condensateur, tu seras invincible 
D'accord, c'étaient bel et bien les intégrales qu'il fallait utiliser, mais comme nous n'avons pas encore abordé ça en physique je me sentais bien perdue ! 
Tes explications semblent me convenir, merci bien, je vais essayer d'appliquer tout ça. 
Bon je bloque justement pour le passage à la plaque B du condensateur.. 
Parce qu'on ne peut pas considérer ici que t=0, mais justement, je ne sais pas trop si je peux mettre t=1..
Pour le raisonnement (q.2)b.) , j'utilise le même que pour la première vitesse mais en changeant juste la valeur t ?
Bonjour
Tes explications semblent me convenir
J'apprécie ton sens de la mesure

Dans l'énoncé il est dit que:
Un électron arrive en O avec la vitesse v1 de direction (Ox) à la date t0=0
On définit donc un nouveau référentiel, avec une nouvelle mesure du temps, t0, avec t0 = 0 à l'arrviée de l'électron entre les plaques du nouveau condensateur.
By the way, aurais tu la possibilité d'attacher le schéma à ce post histoire de s'assurer que nous parlons des mêmes repères.
Les conditions initiales de la 2eme phases (t0 = 0) sont
Ensuite, c'est le même raisonnement que précédemment avec cette fois une accélération selon l'axe Oz
Donc:
Le suite n'est plus qu'une histoire d'intégration le long d'une variable t0 ...
Courage!
Voici le schéma associé à l'exercice du bouquin : on remarque le repère (z; O; x1)
Je vais tenter d'avancer avec les explications données, merci encore 
Merci pour ce schéma.
Donc dans la question 3) on considère que C1 est hors tension et que l'électron arrive au condensateur C2 avec la vitesse v1 qu'il avait en traversant la plaque B:
Je remarque d'ailleurs que je ne t'ai pas "aidé" à répondre à la question 2)b) qui demande de déterminer v1. Et comprends mieux ta question:
Pour le raisonnement (q.2)b.) , j'utilise le même que pour la première vitesse mais en changeant juste la valeur t ?
On a vu précédemment que:
avec
(note: UAB est négative, donc x1 et v1 sont bien positives)
en éliminant la variable t entre les 2 premières équations:
Donc pour x1 = dAB:
Bon je crois que maintenant on est "raccord". Désolé pour ce contre temps, comme quoi un schéma aide à clairfier surtout lorsque l'on ne fait pas des exos sur les oscillos tous les jours

Pour répondre à 3) tu considères donc qu'à t = 0 l'électron quitte le 1er condensateur et qu'il entre dans le champs E2 du condensateur à un instant t1.


