Inscription / Connexion Nouveau Sujet
DM "Canon à électrons"
Bonjour tout le monde, j'ai un dm de physique à faire pour la rentrée et je suis bloqué sur certains points.
Voici l'énoncé :
"Un canon à électrons est constitué d'un filament qui, lorsqu'il est porté à haute température, émet des électrons de vitesse initiale négligeable. Ces électrons sont ensuite accélérés à l'intérieur d'un condensateur plan dont les armatures A et B sont veticales et entre lesquelles règne un champ électrostatique uniforme de valeur E.
Schéma :
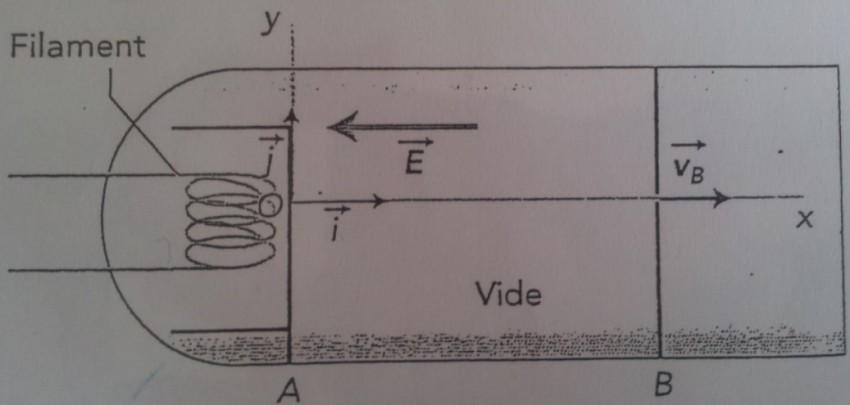
On négligera le poids de l'électron devant la force électrostatique. Le référentiel est supposé galiléen."
Questions :
1/a. Déterminer les coordonnées du vecteur accélération et du vecteur vitesse vitesse
de l'électron au cours du mouvement entre les plaques A et B. On choisira le repère (O;
;
) indiqué sur le schéma.
Je ne vois pas comment faire pour répondre à cette question...
b. En déduire l'expression de la valeur de sa vitesse à chaque instant.
Voici ma réponse :
(car
est négligable devant
)
Soit :
Donc on a :
2/ Déterminer les équations horaires de son mouvement.
D'après les réponses précédentes, j'ai :
Donc au final on a :
(car
Donc
3/a. Montrer que l'expression de la vitesse de l'électron lorsqu'il parvient à la plaque B du condensateur est :
Pour cette question, je ne vois pas par "où commencer" et je suis un peu perdu...
b. Calculer la valeur de de cette vitesse.
Données :
De ce fait j'obtiens
Même pour une simple application numérique je ne suis pas sûr de mes résultats, car ces valeurs me semblent beaucoup trop grandes, et je me demande si il n'y a pas un piège au niveau des unités des valeurs données...
Merci d'avoir lu mon long message, et bien sûr je n'oublie pas de le demander : "un peu d'aide svp ?" 
vect a = (e * E/m ; g)
Et puisque on peut négliger l'effet du poids, vect a = (e * E/m ; 0)
vx(t) = e.E/m * t (puisque Vo = 0 car l'énoncé précise : ...émet des électrons de vitesse initiale négligeable)
vy(t) = 0
x(t) = e.E/m * t²/2 (puisque l'origine du repère dessiné est tel que x(0) = 0)
y(t) = 0 (puisque l'origine du repère dessiné est tel que y(0) = 0)
-----
vB:
x = 0,03 m
e.E/m * t1²/2 = 0,03
1,6.10^-19 * 6.10^4/(9,11.10^-31) * t1²/2 = 0,03 ---> t1 = 2,386.10^-9 s
vB = e.E/m * t1 = 1,6.10^-19 * 6.10^4/ (9,11.10^-31) * 2,386.10^-9 = 2,51.10^7 m/s
(10 fois plus petit que ta réponse ... )
-----
Sauf distraction. 
D'accord, merci pour ton aide, j'ai bien compris ce qui etait faux dans mes réponses 
Mais aurait tu l'amabilité de bien vouloir m'aider sur les autres questions où je bloque stp ?
Bonjour,
C'est bien commencé, mais cela bifurque brusquement sans explication...
Je suis d'accord jusque :
Donc au final on a :
Soudain apparaît un y ... d'où vient-il ?
_________
Tu as l'expression correcte de la vitesse :
Tu as aussi l'expression correcte de l'équation horaire :
Il est donc très facile d'en déduire V(x) et en particulier V(d), ce qui répondra à la question 3a
_________
En effet, la vitesse calculée est trop grande.
Il n'y a pas de piège avec les unités. Quelle est l'unité de longueur dans le système international d'unités ? Est-ce bien ce que tu as utilisé ? Non, d'après ton résultat...

Bonjour Coll,
____________________________________________________________
Donc si je comprends bien, V(d) = V (3.00*10^-2) ?
Et donc je pose V(3.00*10^-2) =
Mais cependant, je ne connais pas la valeur de "t"
Donc il faut que j'isole mon "t" dans l'expression précédente, et refaire l'application numérique pour ainsi obtenir
Est ce que je suis sur la bonne voie ?
___________________________________________________________
Du coup en refaisant l'application numérique j'obtiens : 25145023.93 m/s
_____________________________________________________________
Et "l'apparition" de mon "y" c'est l'équation de la trajectoire en fonction de la valeur de x
Est ce faux ?
Oui, tu es sur la bonne voie.
Il faut chercher t en fonction de x
puis remplacer t dans l'expression de la vitesse
Et tu obtiens ainsi V en fonction de x
__________
ay = 0
vy(t) = 0
y(t) = 0
La trajectoire est l'axe Ox
Il n'y a pas de y(x) = ... pour la trajectoire ; rien d'autre que y(x) = 0
__________
Oui, en exprimant d en mètre d = 3.10-2 m
tu obtiens la vitesse correcte.
Attention de ne pas annoncer 10 chiffres... quand seuls les trois premiers peuvent être significatifs.

Okay très bien, merci pour ton aide 
Je me replongerai sur mes exos demain et je te montrerai ce que ça donne !
D'ici là, bonne soirée et encore merci ! 
Bonjour, me revoici !
alors j'ai quasiment finis tout le DM, malheureusement, je suis coincé et j'arrive presque au résultat souhaité pour la question 3/a.
Voici mon calcul :
Ainsi on a :
Après, il faut que je retombe sur l'expression de :
ce qui n'est pas une mince affaire....

Donc, mes questions sont :
Est ce que je pars de la bonne formule à simplifier ?
Ou, est ce que j'ai un problème de méthodologie et dans ce cas là pourriez vous m'aider svp ?
C'est bien parti...
Une faute d'inattention :
Ce qu'il faut simplifier (et ce n'est qu'une "mince affaire")

Bonjour,
je pense que je touche presque au but avec cette simplification d'expression.
Cependant il me reste un point à éclaircir dans la question 1/a.
Lorsqu'il est demandé dans la question 1/a. les coordonnées du vecteur accélération (a) et du vecteur vitesse (v), est ce qu'il s'agit bien des expressions suivantes ?



