Inscription / Connexion Nouveau Sujet
Dipole RC en charge
bonjour,
encore un post pour savoir si vous pouviez m'aider pour résoudre quelques question de qcm non corrigé que j'utilise pour m'entrainer à un concours.
j'ai essayer de répondre mais j'ai du mal et je crois que mes réponses ne sont pas les bonnes.
Enoncé:
entre t=0 et t=T/2 la tension du générateur est E
entre t=T/2 et t=T la tension du générateur est -E
entre t=T et t=3T/2 la tension du générateur est E
entre t=3T/2 et t=2T la tension du générateur est -E
et ainsi de suite.
on a E=6V et la fréquence f de cette tension est réglable.
on observe alors aux bornes du condensateur la tension Uc suivante:
entre t=0 et t=T/2 Uc passe de -U1 à U1
entre t=T/2 et t=T Uc passe de U1 à -U1
et ainsi de suite.
On se propose ici de déterminer la valeur de la capacité C d'un condensateur avec ce type de manipulation. Pour cela, on utilise un résistor de résistance R=1,00 k (valeur mesurée à l'aide d'un ohmmètre) et pour différentes périodes T, on mesure au bout de quelques secondes la valeur maximale U1 de la tension aux bornes de C. Les résultats sont les suivants:
(valeur mesurée à l'aide d'un ohmmètre) et pour différentes périodes T, on mesure au bout de quelques secondes la valeur maximale U1 de la tension aux bornes de C. Les résultats sont les suivants:
| T | 10 ms | 1 ms | 100  s s | 10  s s | 1  s s |
| U1 | 5,92 V | 1,47 V | 150 mV | 15 mv | 1,5 mV |
Pour les calculs suivants, on appelle que si un condensateur a une tension U0 à ses bornes à la date t=t0 et qu'on le charge à travers une résistance à l'aide d'un générateur de force électromotrice constante UE, la tension u aux bornes du condenstaeur varie avec le temps t comme u(t)=E+(U0 - UEe-(t-t0/
 )),
)),  étant la constante de temps du circuit de charge précédent.
étant la constante de temps du circuit de charge précédent.
Question 1:
Si le condensateur est déchargé à t=0, (attention ce n'est pas le cas dans la description du début), la tension à ses bornes à la date T est (en valeur absolue):
a- -E
b- -E*(T/2RC)
c- -E(1-e-T/(2RC))²
d- -E(1-e-T/(RC))
Personnellement j'ai répondu la D, meme si le "-" me dérange... cependant cela reste la seule réponse qui correspond au cours.
Question 2:
Au moment de la mesure de U1, la tension aux bornes de C est:
a- alternative
b- sinusoïdale
c- triangulaire
d- c'est l'intégrale du signal délivré par le générateur
Personnellement j'ai répondu que ca correspondait à l'intégrale du singal délivré par le générateur. déduction fait à partir du graphique de l'évolution de la tension aux bornes du condensateur, que je n'ai malheureusement pas pu vous communiquer.
Question 3:
L'expression de la tension U1 est:
a- U1=E*(T/4RC)
b- U1=(RCET)/4
c- U1=E(1-e-T/(RC))
d- U1=E*[(1-e-T/(2RC))/(1+e-T/(2RC))]
Pour moi la bonne réponse est la C toujours en se référant au cours.
Question 4:
la valeur de C est:
a- 100 nF
b- 300 nF
c- 1,00
 F
F
d- 3,00
 F
F
Pour répondre à cette question je pense qu'il faut utiliser le tableau de valeurs et du coup en déduire la valeur de
 , puis en utilisant la formule
, puis en utilisant la formule  =RC en déduire C.
=RC en déduire C.3)
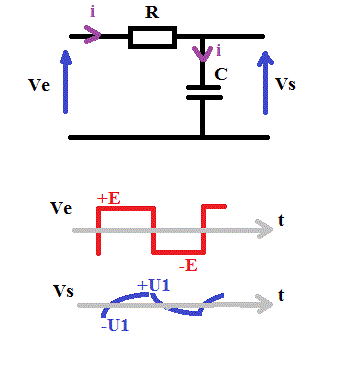
Considérons t = 0 au moment du flan montant de Ve, on a alors Ve = +E pendant une durée T/2.
Et on a Vs(0) = -U1 et Vs(T/2) = +U1
Pour t dans [0 ; T/2], on a donc :
i = (E - Vs)/R
i = C.dVs/dt
(E - Vs)/R = C.dVs/dt
RC dVs/dt + Vs = E
Equation différentielle qui résolue donne :
Vs(t) = K.e^(-t/(RC)) + E (avec K une constante réelle à déterminer).
Comme Vs(0) = -U1, ion a : -U1 = K + E
K = -U1 - E
--> Vs(t) = (-U1 - E).e^(-t/(RC)) + E
Vs(t) = -U1.e^(-t/(RC)) + E.(1 - e^(-t/(RC))
Mais on a aussi Vs(T/2) = +U1 et donc :
U1 = -U1.e^(-T/(2RC)) + E.(1 - e^(-T/(2RC))
U1.(1 + e^(-T/(2RC)) = E.(1 - e^(-T/(2RC))
U1 = E.(1 - e^(-T/(2RC))/(1 + e^(-T/(2RC))
Et donc c'est la réponse d qu'il faut cocher.
-----
Sauf distraction. 
Merci beaucoup J-P. ^^ je vais travailler ça de suite.
PS: étant donné que vous n'avez fait aucun commentaire sur les autres questions, est-ce que je peux en conclure que j'ai donné les bonnes réponses?
vu que je ne suis pas sur de moi, j'aurais aimé une confirmation ou infirmation.
cordialement.
4)
Comme la réponse à la question 3 est : U1 = E.(1 - e^(-T/(2RC)))/(1 + e^(-T/(2RC)))
Il suffit de remplacer E par 6 Volts, R par 1000 ohm et de remplacer U1, et T par un couple de valeurs tirées du tableau ... et enfin calculer la valeur de C.
Exemple : T = 100 µs et U1 = 150 mV --->
0,15 = 6*(1 - e^(-10^-4/(2000.C)))/(1 + e^(-10^-4/(2000C)))
0,15 = 6*(1 - e^(-5.10^-8/C))/(1 + e^(-5.10^-8/C))
0,025 = (1 - e^(-5.10^-8/C))/(1 + e^(-5.10^-8/C))
0,025 (1 + e^(-5.10^-8/C)) = (1 - e^(-5.10^-8/C))
0,975 = 1,025.e^(-5.10^-8/C)
e^(-5.10^-8/C) = 0,9512
-5.10^-8/C = ln(0,9512)
C = -5.10^-8/ln(0,9512)
C = 10^-6 F
Et donc C = 1 µF
----
Ici, avec un poil de feeling, on trouve la réponse sans faire ce long calcul.
Comme U1 < < E, on a pratiquement I = E/R = 6 mA
et I = C.dU/dt ---> 6.10^-3 = C * 2U1/(T/2)
6.10^-3 = C * 2*015/(10^-4/2)
C = 10^-6 F
C'est un calcul approché, mais tout à fait "légitime".
-----
Sauf distraction. 


