Inscription / Connexion Nouveau Sujet
Deux mobiles (lois de la dynamique)
Bonsoir à tous
alors voila mon énonce:
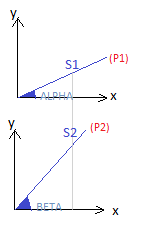
deux solides ponctuels S1 de mase m1 et S2 de masse m2glissent sans frottement respectivement su les plans inclinés P1 et P2. L'axe des abscisses correpond à l'horizontale; l'axe des ordonnées correspond à la verticale. On lache S1 et S2 simultanément et sans vitesse initiale de deux point de meme abscisse x=4m.
données: m1=2kg; BETA=45°; m2=1kg
pour quelle valeur de l'angle ALPHA les énergies cinétiques aux origines O1 et O2 seront elles égales?
Bon j'ai effectué les recherches des deux delta d'énergies cinétiques en y incorporant bien sur les angles ALPHA et BETA et je trouve ALPHA = 26,6 °
Alors que ma correction me donne pour réponse (sans aucunes explications): ALPHA = 30 °
je sais que ce livre se trompe régulièrement, je voulais savoir si tel était le cas et quel résultat vous trouveriez.
En espérant vous lire vite, bonne soirée 
Salut krinn merci pour te contribution à 1h du mat
Mais je ne comprend pas du tout ce que veux dire arctg
bonjour,
oui, j'utilise parfois des notations qui datent un peu, effectivement.
au lieu de a
arctg au lieu d' arctan si j'ai bien lu: 
donc ici: tg alpha = 1/2
ou encore: alpha = arctan(1/2)
Désolé de te décevoir mais je n'ai pas vus ce chapitre.
Concrètement combien trouves tu de degré pour l'angle ALPHA?
La bonne réponse est alpha = 26,6°
Celui qui a fait la correction a sûrement confondu une tangente avec un sinus.
Il reste à faire une quête pour payer des cours de recyclage au correcteur.
Mobile 1 :
Soit X l'abscisse de départ.
L'ordonnée correspondante est Y1 = X.tan(alpha)
E cinétique en O1 : Ec1 = m1.g.Y1 = m1.g.X.tan(alpha)
-----
Pareillement pour le mobile 2 :
E cinétique en O2 : Ec2 = m2.g.X.tan(beta)
-----
On aura Ec1 = Ec2 pour : m1.g.X.tan(alpha) = m2.g.X.tan(beta)
m1.tan(alpha) = m2.tan(beta)
tan(beta) = (m2/m1).tan(beta)
tan(beta) = (1/2).tan(45°)
tan(beta) = 1/2
beta = arctan(1/2) = 26,6° (arrondi)
-----
Annuler
connectez vous