Inscription / Connexion Nouveau Sujet
déterminer les caractéristiques du vetcteur accélération
Bonjour, je bloque sur un exercice type: J'ai la correction mais ne comprend toujours pas:
Un objet de masse m se déplace sans frottement sur un plan incliné (l'objet descend) ; ce plan
est incliné d'un angle "alpha" par rapport au plan horizontal.
1 - Exprimer les caractéristiques du vecteur accélération aG du centre d'inertie. (On donnera
la valeur de aG en fonction de g et "alpha"
Dès que le plan est incliné, je ne comprend plus comment faire....
Merci de m'aider!
Bonjour,
Quel est le référentiel ?
Quelles sont les deux forces ?
Quel est le repère qui convient bien pour la projection de ces deux forces ?
Que vaut la somme vectorielle (la résultante) de ces deux forces ?
Quelle est la loi de Newton qui s'applique ?

Merci de m'avoir répondu! 
-Référentiel galiléen: référentiel terrestre
-Bilan des forces:
Vec R (réaction du sol)
Vec P (poids. P=mg)
-le repère, c'est là que je bloque (comme c'est incliné...)
-D'après la 2nd loi de Newton: somme des Forces extérieures = m(Vec)a
D'où m(Vec)a = (Vec)P + (Vec R)
...
Il va falloir être plus précis pour les forces.
On ne définit pas une force par un nombre (un scalaire ; comme on peut le faire avec la masse par exemple). Pour définir une force, que l'on représente en physique par un vecteur, il faut quatre caractéristiques :
. son point d'application
. sa direction
. son sens
. son intensité
Quelles sont les quatre caractéristiques du poids ?
Quelles sont les trois premières caractéristiques de la réaction du support ?

le point d'application du poids est le centre d'inertie de l'objet?
sa direction verticale
son sens est dirigé vers le centre de la terre
et son intensité est... ??
si le plan était horizontal, je dirai que les caractéristiques de R sont les mêmes que P sauf le sens: c'est l'inverse; et le oint d'application qui est le sol
Mais comme c'est un plan incliné, cela a t'il un rapport avec le cosinus "alpha"
je suis désolée mais je ne vois pas où vous voulez en venir...
Mais merci de m'aider 
En physique on devrait toujours commencer par un dessin.
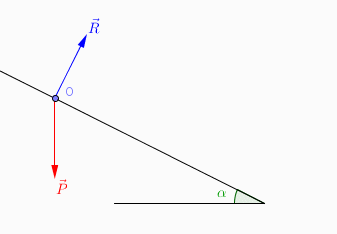
Je suis tout à fait d'accord pour le poids :
. point d'application le centre de gravité de l'objet (considéré comme ponctuel dans tous ces problèmes) : ici le point O
. direction : la verticale
. sens : vers le bas (vers le centre de la Terre)
. intensité = m.g
Pour la réaction du support
. point d'application : le même point O
. direction : ...
. sens : ...
Où je veux en venir ? À ce que tu comprennes comment faire ce genre de problème ! !

R
direction: normale à la trajectoire
sens: ... (ce n'est pas le sens contraire de P puisque R et P n'ont pas la même direction...)
Direction : perpendiculaire au support
Sens : vers l'extérieur du support (ou encore, vers le haut)
Je te propose les axes du repère Ox et Oy
Ox : parallèle au plan incliné, dans le sens de la descente et donc dans le sens du mouvement
Oy : perpendiculaire au plan incliné, vers le haut
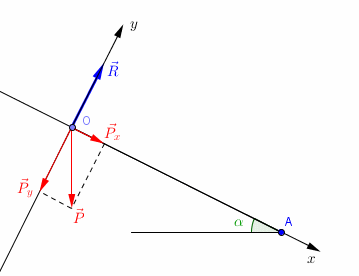
On va projeter les vecteurs et
sur ces axes Ox et Oy
Cela est particulièrement facile pour le vecteur
Et il faudra un tout petit peu de trigonométrie pour projeter le vecteur afin de connaître ses deux composantes
et
, sachant que la composante qui nous intéresse le plus est
Que valent donc

Donc,
Vec Rx = Vec 0
Vec Ry = Vec Ry (comment l'exprimer autrement?)
Vec Px
on a sin "alpha" = côté opposé / hypothénuse
DONC sin "alpha" = Px / mg
D'OU Vec Px = sin "alpha" * m * Vec G
Vec Py
cos "alpha" = Py / mg
DONC Vec Py = cos "alpha" * m * Vec g
Très bien !
Ce qu'il faut absolument retenir c'est l'égalité de ces trois angles en vert :
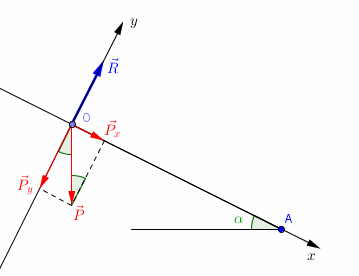
Si je note  le vecteur unitaire de l'axe Ox et
le vecteur unitaire de l'axe Ox et  le vecteur unitaire de l'axe Oy, je peux écrire :
le vecteur unitaire de l'axe Oy, je peux écrire :
____________
Application du principe fondamental de la dynamique :
Le produit de la masse par l'accélération est égal à la somme des forces appliquées
Mais...
et
donc... que vaut ?

Vec a = Vec Px
d'où Vec a = m.g.sin "alpha" Vec i + 0 Vec j
donc Vec a ne s'exprime qu'en fonction de l'axe Ox

c'est ça?
Pas tout à fait ; tu as oublié la masse :
et donc :
L'accélération est dirigée selon le plan incliné, dans le sens de la descente et son intensité vaut

D'accord...
m Vec a c'est la seconde loi de Newton?
on a:
m Vec a = Vec P + Vec R
<=> m Vec a = m.Vec g.sin "alpha"
d'où Vec a = g.sin "alpha" Vec i
?
Merci beaucoup pour vos explications!
le fait que vous m'ayez guidé va me permettre de retenir plus facilement!!
J'ai (enfin) compris donc merci beaucoup!



