Niveau terminale

Cyclotron.

Posté par
kamikaz 18-04-21 à 06:43

Bonjour ,

Merci d'avance.

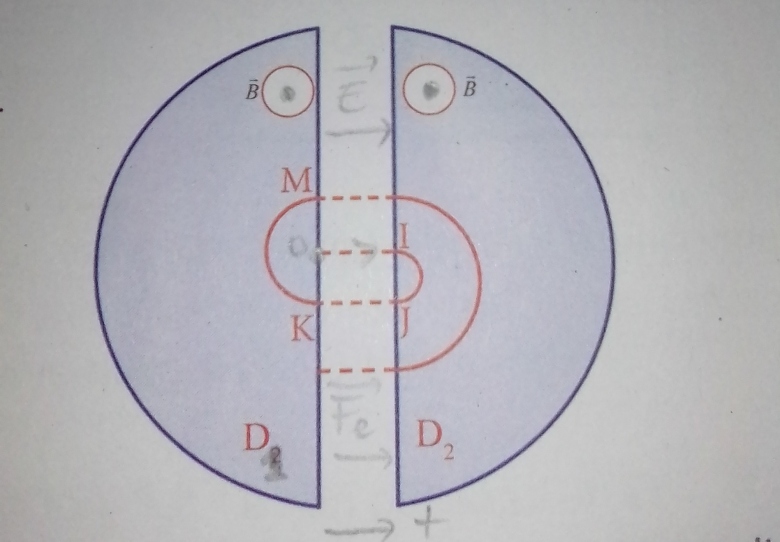
Le clotron permet d'accélérer des particules chargées pour produire de l'énergie. Il est constitué de deux enceintes demi-cylindriques D₁ et D₂ appelées <<dées>> placées horizontalement dans un champ magnétique uniforme vertical (voir figure).

Dans l'espace compris entre D, et les protons qui doivent être accélérés sont soumis un champ electrique alternatif $\vec{E}$ de façon à être accélérés à chaque passage.

Les protons sont émis au point O avec une vitesse négligeable. Ils décrivent à l'intérieur
des <<dées>> un mouvement circulaire uniforme.

Données : masse d'un proton : m=1.67.10 kg ;

Charge proton = 1,6.10^-19 C ;

B=1,5 T ;

U = 1000 V rayon moyen des <<dées>> ;

R = 0.8 m

Cyclotron.

1) Préciser :

1-1) La direction et le sens du vecteur champ électrique $\vec{E}$ pour qu'un proton soit accéléré entre les points O et I.

1-2) Le sens de B sur la figure pour obtenir le sens de rotation indiqué.

2) Determiner

2-1) La vitesse $v_{1}$ d'un proton en l en fonction de e , U et m.

2-2) La vitesse $v_{2}$ d'un proton en K en fonction de e, U et m (lorsqu'il a fait un tour).

2-3) L'expression du rayon de la trajectoire IJ.

2-4) L'expression de la vitesse d'un proton après n tours.

3) Déterminer l'énergie maximale d'un proton connaissant le rayon moyen R des <<dées>>.

Réponses

1-1) Précisons les directions et le sens de $\vec{E}$ .

$\vec{F_{e}}=q\vec{E}$

q > 0 ==> $\vec{F_{e}}$ et $\vec{E}$ sont de même sens , même direction.

1-2) Sens de $\vec{B}$ .

$\vec{F_{m}}=q\vec{v} \land \vec{B}$ .

Le sens de $\vec{B}$ est tel que $\left(q\vec{v} ; \vec{B} ; \vec{F_{m}}\right)$ soit direct donc $\vec{B}$ est sortant (règle de la main droite).

2-1) La vitesse en f(e , U ,m).

* Système : le proton.

* Référentiel : Terrestre supposé galiléen.

* Bilan des forces extérieures : La force électrostatique $\vec{F_{e}}$ .

Représentation : voir figure.

Application du théorème de l'énergie cinétique :

$\Delta_{O \mapsto I}=\sum W_{O \mapsto I} (\vec{F}_{\text{ext}})$

$EC_{I}-EC_{O}=W_{O \mapsto I} (\vec{F_{e}})$

$\dfrac{1}{2}mv_{1}²-\dfrac{1}{2}mv_{2}²=q(v_{P}-v_{N})$ or v_O= 0 , q=e et v_P -v_N=U.

==> $\dfrac{1}{2}mv_{1}²=eU$

$v_{1}=\sqrt{\dfrac{2eU}{m}}$

2-2) Vitesse v₂ en f(U , e , m)

$\Delta_{I \mapsto K}=\sum W_{I \mapsto K} (\vec{F}_{\text{ext}})$

$EC_{I}-EC_{K}=W_{O \mapsto I} (\vec{F_{e}})$

$\dfrac{1}{2}mv_{2}²-\dfrac{1}{2}mv_{1}²=q(v_{P}-v_{N})$ or v_O= 0 , q=e et v_P -v_N=U.

==> $\dfrac{1}{2}m(v_{2}²-v_{1}²)=eU$

$v_{2}²=\dfrac{2eU}{m}+v_{1}²$

$v_{2}=2sqrt{\dfrac{eU}{m}}$

2-3) L'expression du rayon de la trajectoire IJ.

* Système : Le proton

Référentiel : Terrestre supposé galiléen.

Bilan des forces extérieures : Force de Lorentz $\vec{F}$ .

Application du théorème du centre d'inertie.

$\sum \vec{F}_{ext}=m\vec{a}$

$\vec{F}=m\vec{a}$

$q\vec{v_{1}} \land \vec{B}=m\vec{a}$

$\vec{a}=\dfrac{q\vec{v_{1}} \land \vec{B}}{m}$

(1) : $a=\dfrac{qv_1 B}{m}$ car $\vec{v}$ $\vec{B}$

Le mouvement des protons étant circulaire uniforme ; $a=a_1 =\dfrac{v_1 ²}{R}$ (2)

(1) et (2) ==> $\dfrac{v_1²}{R}=\dfrac{qv_1 B}{m}$

==> $R=\dfrac{v_1²m}{qv_1B}$

==> $R=\dfrac{v_1 m}{eB}$

==> $R=\dfrac{m}{eB}\sqrt{\dfrac{2eU}{m}}$

==> $R=\dfrac{1}{B}\sqrt{\dfrac{2em²U}{me²}}$

==> $R=\dfrac{1}{B}\sqrt{\dfrac{2mU}{e}}$

2-4) Expression de V_n.

*1er passage en I ==> $\Delta EC = \sum W(\vec{F})$

$EC_1=1eU$

*2e passage en I ==> $\Delta EC =\sumW(\vec{F})$

$EC_2-EC_1=eU \Rightarrow EC_2 =eU+EC_1$

$EC_2=eU+eU$

$EC_2=2eU$

.
.
.
n ième passage en I ==> $EC_n =neU$

$v_n=\sqrt{\dfrac{2neU}{m}}$

3) Je ne vois pas vraiment comment faire..

Posté par re : Cyclotron. 18-04-21 à 09:44

Bonjour kamikaz,

L'exercice a déjà reçu une correction ici : mouvement d une particule chargée dans un champ magnétique unifo

En tout cas, je tiens à te féliciter pour la qualité rédactionnelle de cet exercice, je n'ai rien à ajouter, on voit un grand progrès entre tes sujets d'il y a quelques mois et ceux aujourd'hui.

Posté par re : Cyclotron. 18-04-21 à 13:38

Merci

Posté par re : Cyclotron. 18-04-21 à 17:23

Je t'en prie, bonne fin d'après-midi !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cyclotron.

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique