Inscription / Connexion Nouveau Sujet
Cyclotron 1
Bonjour, aidez-moi svp.
Problème :
On donne : masse du proton m = 1,67.10-27kg ; charge élémentaire e = 1,6.10-19 C ; d = 1 cm ; U = 4000 V.
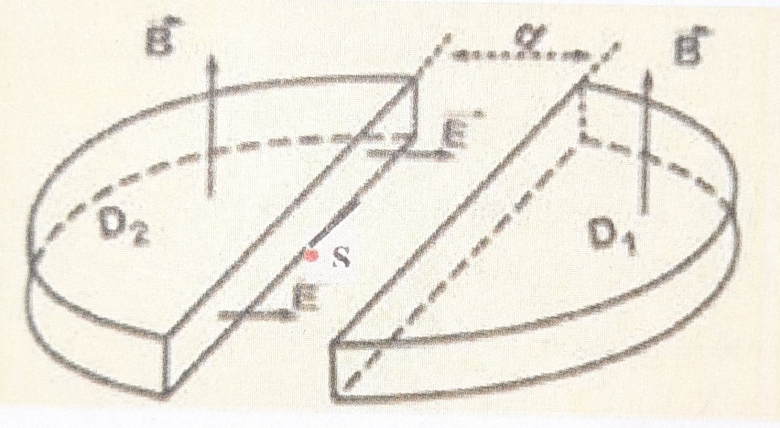
Un cyclotron est un dispositif constitué de deux demi-cylindres D1 et D2 séparés par une distance très faible d devant leur diamètre. Le tout est placé dans le vide. Un champ magnétique perpendiculaire au plan de la figure est créé dans D1 et D2. Une source S (Voir croquis) émet des protons dont la vitesse initiale est nulle. Entre les deux demi cylindres (《dees》) et sur la distance d agit un champ électrique uniforme
.
est constamment nul à l'intérieur des 《dees》.

Question 1)
Le Théorème de l'énergie cinétique appliqué sur le proton en mouvement dans le champ électrique donne :
Seule la force électrique est appliquée, le poids du proton est négligeable.
½mV1² = eU 
AN : V1  8,75.105 m/s
8,75.105 m/s
OK. Pour la suite, il faut démonter que le mouvement est circulaire uniforme. Cela se fait en 4 étapes :
1° : le mouvement est plan (perpendiculaire au vecteur champ magnétique) ;
2° : le mouvement est uniforme ;
3° : le mouvement est circulaire uniforme ;
4° : expression du rayon de trajectoire.
2.a) Expression du rayon R1
- système : proton de masse m ;
- référentiel : terrestre (supposé galiléen) ;
- bilan des forces : le poids et la force magnétique
Je demande le code pour taper le produit vectoriel.
Mais le poids est négligeable devant la force magnétique.
Le TCI donne : (1)
Soit un repère orthogonal de projection tel que
est parallèle à
et de même sens.
Selon la relation (1) : est perpendiculaire à
, mais
est parallèle à l'axe (Oz), ce qui implique que
est perpendiculaire à (Oz). Donc
Par intégration successive de aZ, on trouve Z = 0.
La côte Z étant nulle, le mouvement est plan. La trajectoire est située dans le plan XOY.
• la puissance de la force magnétique est : ( car
est perpendiculaire à
D'autre part, la puissance est :
En appliquant le TEC entre l'instant où la particule pénètre dans le dee D1 et l'instant où elle sort, on obtient :
Le mouvement est donc uniforme.
• selon l'expression du vecteur accélération, est perpendiculaire au vecteur vitesse
à chaque instant. Donc
est normal. Le mouvement est Circulaire.
• Expression du rayon :
étant normal, je pose :
En remplaçant a par son expression on trouve enfin :
Merci bien.
Maintenant j'écris :
Je remplace
Donc
2.b) Temps de transit du dee D1
Le mouvement dans un dee étant circulaire uniforme, le temps de transition dans un dee est la durée d'un demi-tour. C'est la moitié d'une période (durée d'un tour complet)
AN :  = 31,8 ns
= 31,8 ns
Ce temps est trop petit vanoise.
Résultat correct. On applique entre les dees une tension accélératrice de fréquence relativement élevée.
3.a) le temps de transit dans un temps étant indépendant de la vitesse du proton, je trouve toujours pour le dee 2 :
AN :  = 31,8 ns
= 31,8 ns
comparaison des temps : le temps est le même.
3.b) Description du mouvement :
Le temps de transit de le champ électrique était trop faible (tension accélératrice grande), le mouvement du proton dans un dee est circulaire uniforme.
Dans chaque dee, le mouvement de la particule est bien circulaire et uniforme mais cela n'a rien à voir avec le fait que la durée d'un demi tour reste constante. Quand n augmente, le rayon de trajectoire augmente mais, comme la vitesse augmente proportionnellement, on obtient une durée indépendante de n. Cela présente un intérêt pratique. La tension accélératrice peut être obtenue en reliant les deux dees aux deux bornes d'un générateur de tension sinusoïdale dont on pourrait déterminer la fréquence...
3.c) Calcul de la quantité V22-V12
Application de TEC entre les dees :
 Ec =
Ec =  W(Fex
W(Fex
Donc
Alors
Maintenant, quand je fais l'application numérique, je trouve ceci :
V22- V12 = 7,66.1011 m2.s-2
Déduisons-en V32, puis V42
De la relation , on tire :
De même
En remplaçant V22 par son expression, on trouve :
Alors V4² devient :
Et ainsi de suite....
Question 3.d)
Donc
Donc on déduit que
Ainsi R2 sera
En remplaçant V2 par son expression et en arrangeant la relation, je trouve :
Et aussi
Et ainsi de suite...
Calculons n pour Rn = 0,14 m
À partir de la dernière relation, on a
Avec
D'où
J'ai trouvé n = 1,6.10-7 , résultat qui ne me convient pas du tout 
Ohhh merci, j'ai vu l'erreur !
Je retravaille, puis je reviens.
J'étais absent tout ce temps là, j'ai changé de téléphone, maintenant j'utilise un iPhone 12 Pro Max. Quand je tape un code dans l'éditeur de codes LtX puis je l'insère, il m'est impossible de revenir ensuite dans la zone de texte. Je ne sais pas si le cas est général pour tous les iPhone.
Avant j'utilisais un Samsung et c'était vraiment simple et rapide de revenir dans la zone de texte.
Présentement, pour taper une formule dans le LtX, je suis obligé de prendre le téléphone de mon jeune frère.
Y'a-t-il une solution pour ça ?
Question 3.d)
(Mais V2 = V1
 2)
2)
Alors
Donc par déduction
Au nieme tours
D'où
Maintenant, pour Rn = 0,14 m, je trouve :
n = 249 tours.
Ce résultat me semble vraisemblable 
La vitesse correspondante se calcule par la relation :

AN : Vn = 1,38.107 m/s
Maintenant il me reste la dernière question
D'accord. Tu constates aussi que v2 nettement inférieur à c2. La mécanique classique de Newton s'applique en excellente approximation sans correction relativiste.
Question e)
• au 1er tour :  Ec = 2qU
Ec = 2qU
• au 2e tour :  Ec = 2*2qU
Ec = 2*2qU
.
.
.
• au nième tour :  Ec = 2nqU
Ec = 2nqU
Sachant que la vitesse initiale d'injection des protons est nulle, au nième tour,  Ec = (1/2)mVn2
Ec = (1/2)mVn2
Alors
AN : U = 1995,7 V
Il s'agit à la dernière question de déterminer la tension Uo (pas U puisque cette lettre désigne la tension entre les dees) qui, appliquée entre deux plaques, produit la même vitesse finale que le cyclotron.
Cette tension vérifie :
½m.Vn2=e.Uo
Cela conduit à :
Uo=n.U
Logique puisqu'il s'agirait d'obtenir en une seule fois, la vitesse obtenue avec le cyclotron avec n accélérations successives. Une telle tension est impossible à obtenir dans un accélérateur de particules, d'où l'intérêt du cyclotron.
PS : j'ai laissé passer précédemment une imprécision. On obtient bien n=249 : il s'agit du nombre d'accélérations successives, donc du nombre de passages d'un dee à l'autre, donc du nombre de demi-tours.
Donc le nombre de demi-tours est n = 249.
Donc le nombre de tours sera n' = n/2 ≈ 125 tours
Pour répondre à la dernière question, je pouvais utiliser la relation
AN : U0 = 6670 V
Maintenant, partant de ton raisonnement U0 = nU
Quelles valeurs de n et U dois-je utiliser ?
Tu ne fais pas bien la différence entre U : la tension accélératrice entre deux dees et Uo : la tension théorique qui, en une seule accélération, ferait passer la vitesse de zéro à la vitesse finale Vn.
Dans le cyclotron ce passage de zéro à Vn est obtenu en n accélérations successives, chacune sous la tension U.
Le théorème de l'énergie cinétique conduit à :
½m.Vn2=n.e.U (formule que tu as déjà utilisée...)
Si la même augmentation de vitesse se faisait en une seule fois, sous l'action d'une tension Uo, le théorème de l'énergie cinétique conduirait à :
½m.Vn2=e.U
Par identification, tu obtiens comme indiqué dans mon précédent message :
Uo = n.U=249x4.103 = 9,96.105V .
Maintenant j'ai bien compris !
Mon problème, c'est que notre professeur nous a parlé du nombre de tours. Il n'a jamais employé le terme « accélération »
Maintenant je comprends, qu'il faut deux accélérations successives pour avoir un tour complet.
J'ai vraiment deux questions sur le cyclotron :
1) Un cyclotron est un accélérateur de particules. Où est-il utilisé précisément ?
2) Est-ce qu'avec un cyclotron de grand rayon utile, avec une très grande tension accélératrice entre les fées, nous pouvons obtenir des particules de très grande énergie cinétique, dont la vitesse dépasse celle de la célérité dans le vide ?
Quelle que soient les performances d'un accélérateur, la vitesse des particules ne peut jamais dépasser c, la vitesse de la lumière dans le vide. Dès que la vitesse de la particule devient non négligeable devant c, la mécanique classique de Newton cesse d'être valide, il faut faire intervenir la mécanique relativiste d'Einstein.
Actuellement, les accélérateurs de particules les plus puissants sont utilisés en recherche fondamentale. Très schématiquement : on fait entrer en collision des particules de très haute énergie cinétique et on étudie le résultat de ces collisions. Cela fournit des renseignements sur les propriétés des particules. Si cela t'intéresse, tu trouves facilement sur le net des informations sur l'accélérateur du CERN situé à côté de Genève.
Un document parmi d'autres : ![]()
Les cyclotrons ne fournissent pas des particules de suffisamment grande énergie pour participer à la recherche fondamentale mais ils sont toujours très utiles, en particulier dans la fabrication de noyaux radioactifs artificiels utilisés en médecine (radiothérapie). Ces noyaux radioactifs sont obtenus en bombardant des noyaux non radioactifs par des protons sortant d'un cyclotron. Un document parmi d'autres :
![]()


