Inscription / Connexion Nouveau Sujet
Coordonnées du vecteur accélération dans un repère
Bonsoir,
Je suis en train de réviser l'application de la seconde loi de newton dans un champ électrostatique uniforme mais je me vois confronté à une petite barrière, que je croyais pourtant avoir dépassé.
Voici l'énoncé :
"Une particule, de masse et de charge q négative, entre dans l'espace entre les deux armatures d'un condensateur plan où règne un champ électrostatique uniforme. Sa vitesse initiale s'écrit :
où les vecteurs i et je sont les vecteurs unitaires des axes (Ox) et (Oy).
Le champ électrostatique s'écrit .
Donc, on procède à la méthode habituelle pour déterminer les équations horaires de x(t) et y(t) du mouvement de la particule.
Cependant, dans l'obtention des coordonnées du vecteur accélération, je suis bloqué mentalement à l'étape :
La deuxième loi de Newton appliquée à la particule s'écrit : .
Or, donc
.
Jusqu'ici tout va bien.
Dans le repère (O;x;y), les coordonnées du vecteur accélération sont :
et
.
C'est ici, que le bât blesse. Je ne comprends pas pourquoi dans l'expression de il n'y a pas de - , car la particule est pourtant chargée négativement.
Voilà ce que me dit la correction : F et a sont orientés vers le bas, mais q est négative d'où le signe + dans l'expression de
Je m'efforce donc de comprendre :
- on est bien d'accord que si q>0, alors , ont même direction et même sens.
- par contre si q<0, alors les deux vecteurs ont même direction mais sens opposés ...
Pourquoi alors marquer que "F et a sont orientés vers le bas mais q est négative d'où le signe + dans l'expression de " ?
Si quelqu'un pouvait m'expliquer cette justification, je lui en serais extrêmement reconnaissant.
Merci !
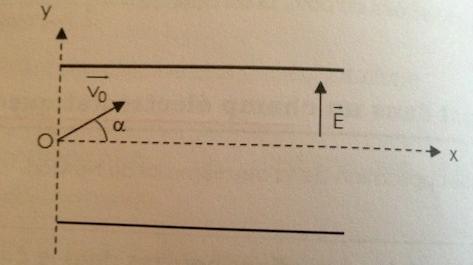
Je me permets de poster la photo du schéma, en pièce jointe :
Merci d'avance pour votre aide !
Edit Coll : image recadrée
Bonsoir,
Je ne vois pas où est ton problème.
Donc, puisque q < 0 les vecteurs et
ont même direction mais des sens opposés
Puisque m > 0 les vecteurs et
ont même direction et même sens.
Ou encore,
Puisque q/m < 0 les vecteurs et
ont même direction mais des sens opposés
dans un sens
et
dans l'autre sens...
D'accord ?

Bonsoir Coll (encore là pour me sauver !),
Je suis tout à fait d'accord avec toi concernant le raisonnement que tu viens de mener.
Mais je ne comprends pas cette histoire de + dans l'expression de
Pourquoi ne s'écrit-il pas :
?
Écriture impossible.
ay est la coordonnée selon l'axe Oy du vecteur ; c'est donc un nombre (un scalaire), positif si le produit scalaire
est positif et négatif sinon
est un vecteur... qui ne peut pas être égal à un scalaire !
Si est de même direction mais de sens opposé à
alors
ay = q.E/m
en notant E la norme (positive) du vecteur
et ainsi ay est un nombre négatif

Mon message de 21 h 20 a croisé le tien de 21 h 17 dans lequel tu rectifiais une erreur. D'accord.
Mais il restait le problème du signe.

Je ne comprends toujours pas pour l'écriture de ne comporte pas de - .
Tu indiques que est un nombre négatif or, la correction indique que
.
En quoi le fait que q soit négatif et que F et a soient orientés vers le bas, permet d'écrire une telle expression de ?
Merci Coll !
Je t'avoue que j'y ai réfléchis longuement tout à l'heure et que je n'ai pas réussi à trouver la réponse.
Peux-tu m'indiquer quelles conditions justement doivent être réunis / quel raisonnement nous amènerait à trouver un signe "-". Je pense que ça m'aiderait dans la compréhension de l'existence du "+".
C'est plutôt bon "signe" (oui...) que tu n'y arrives pas ; car ce serait faux.
_________
En changeant l'orientation de l'axe Oy (vers le bas, au lieu d'être vers le haut), sans changer bien sûr l'orientation du champ et toujours en introduisant une particule de charge q < 0
alors, apparaîtrait un signe moins...
et
seraient bien sûr toujours dirigés vers le bas, et pour que la coordonnée ay du vecteur accélération soit positive, il faudrait un signe "moins"

D'accord, je commence à comprendre !
Donc, dans tous les cas, il faut que la coordonnées (ay) du vecteur accélération soit positive ? Mais pourquoi ?
Sinon, je viens semble-t-il d'avoir l'illumination. Voilà mon raisonnement pour le signe, dis moi ton avis :
Le vecteur champ électrostatique a pour sens les potentiels descendants donc du + vers le -. Sur la figure jointe, on peut donc en déduire que la barre du haut est la barre positive et celle du bas, la barre négative. Le vecteur accélération, est quant à lui, de même direction mais de sens opposé, donc de ce fait, de la borne - vers la borne +. Il est colinéaire avec F car la masse m >0.
Pour moi, E(y) < 0 (peux-tu me confirmer cela ?) et de plus, q<0. Donc, inéluctablement, d'après la relation a(y) = q.E/m ; a(y) est positif car les deux signes - s'annulent.
Qu'en penses-tu ?
Merci 
est de même sens que l'axe Oy, donc Ey est positif
Sur la figure c'est la plaque du bas qui est positive et celle du haut qui est négative.
ay est négatif car q est négatif

Merci pour cette petite astuce concernant le sens de Ey.
D'accord, pour les plaques, je comprends tout à fait.
Le problème : tu dis que ay est négatif, or regarde la pièce jointe, la correction du livre dit qu'il est positif ("d'où le signe + dans l'expression de ay").
Qui a tord, qui a raison ? Je suis perdu !
PS : regarde la pièce jointe (ne fais pas attention à ce qui est marqué au crayon gris).
Merci 
Sais-tu lire ?
Le corrigé dit que q est négative.
Quand on multiplie par un "signe +" quelque chose qui est négatif (q < 0) on a quelque chose qui est négatif. C'est pour cela que ay est négatif, c'est-à-dire orienté vers le bas !

Coll, tu ne réponds toujours pas à ma question !
Ici, ce qui me gène c'est qu'on écrit a(y)=(q/m)E et cette explication hasardeuse du livre qui justifie le signe + dans l'expression de a(y).
Le reste, j'ai tout compris ! Ce qui me gène, c'est l'expression de a(y). Je ne comprends pas pourquoi elle ne comporte pas de - sachant que le vecteur a est orientée vers le bas.
 J'ai déjà répondu une petite dizaine de fois...
J'ai déjà répondu une petite dizaine de fois...
q < 0
donc
- q > 0
cela serait faux puisque le vecteur est orienté dans le sens négatif de l'axe Oy

Bonjour Coll,
Je suis vraiment désolez, mais je ne comprends pas. Je m'arrache les cheveux sur ce détail, alors que je comprends parfaitement tout le chapitre ...
(En tapant ce message, je semble avoir eu l'illumination).
1) En gros, est orienté vers le bas car
. C'est une certitude car
dépend de la charge q.
2) Pour l'écriture de la coordonnée
On a orienté vers le bas (dans le sens négatif de l'axe O(y) ) donc
est négative.
est négatif car
. Donc le fait de rajouter un - serait une hérésie, car cela signifierait que la charge est positive ce qui n'est pas le cas !
Donc a bien la présence du signe + dans l'expression de et pas de -.
Si on avait q=e, on aurait eu alors orienté vers le haut, et donc également :
.
En fait ce qui m'a bloqué, c'est de ne pas voir explicitement un - dans l'écriture de la coordonnée. Or, on peut le considérer comme implicite en quelque sorte car .
Merci Coll pour ta patience et ton explication. J'apprécie beaucoup !
Edit Coll : balise
Eh bien voilà, je suis tout à fait d'accord.
____________
Pour information : il y a une manière plus simple que la tienne pour obtenir un vecteur en :
Pour écrire un vecteur, par exemple le vecteur
. tu tapes \vec{AB}
. tu sélectionnes cela
. tu cliques sur le petit bouton LTX qui se trouve en bas du cadre d'écriture au-dessus de "Aperçu"
. cela place des balises [tex][/tex] autour de la sélection
. comme ceci : [tex]\vec{AB}[/tex]
N'oublie pas de vérifier avec "Aperçu" avant de poster.
____________
Je t'en prie et à une prochaine fois !

D'accord Coll, je te remercie du conseil !
Merci encore une fois de m'avoir aidé sur ce petit détail ... tellement ridicule. J'en ai honte en y pensant.
Bonne soirée et à bientôt !!



