Inscription / Connexion Nouveau Sujet
condensateur
Bonjour j'ai un exo de condensateur dont voici l'énoncé
J'ai essayé de faire la question et je peux avoir de l'aide pour le 2°/ et 3°/. Mais pour le 3°/ je ne comprends pas du tout.
On dispose de plusieurs condensateurs de capacité C1 et C2 : C1=2uF et C2=5uF.
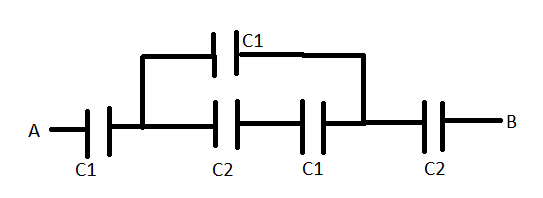
On réalise entre deux points A et B l’association représentée ci-dessous
Calculer la capacité du condensateur équivalent à l’association.
2°/ On dispose de 5 condensateurs de 2uF pouvant supporter chacun 500V.
Déterminer les groupements permettant d’obtenir les capacités suivantes : 1uF ; 2uF ; 3uF ; 4uF ; 5uF ; 6uF ; 7uF ; 8uF ; 9uF ; 10Uf. Quelles sont les tensions maximales à appliquer à chaque groupement ?
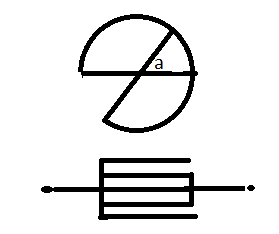
3°/ Un condensateur variable à air C rotatif est formé de 3 lames fixes entre lesquelles peuvent s’engager 2 lames mobiles semi-circulaires de rayon R=3 cm. La distance qui sépare une lame fixe d’une lame mobile est de 0,50 mm. Calculer la capacité du condensateur équivalent lorsque les lames se recouvrent à 180°.
Pour la question 1°/ je sais que que C1, C2, C1 et C2 sont en série donc 1/C=1/C2+1/C2+1/C1+1/C2 et par suite C et C1 sont en parallèle donc Cfinal=C+C1 et pour le reste je suis coincé
Edit Coll : images recadrées
Pour la question 1°/ je rectifie je voulais dire 1/C=1C1+1/C2+1/C1+1/C2
je précise aussi que le schéma 2 concerne la question 3°/ a c'est l'angle
1°/ Il ne faut pas considérer simplement que ces quatre condensateurs sont connectés en série à cause du condensateur supérieur C1 monté en parallèle sur deux de ces quatre condensateurs.
Calcule plutôt le condensateur équivalent aux deux condensateurs situé au milieu de la série de quatre, puis introduis ledit condensateur C1, et calcule enfin l'équivalent des trois condensateurs en série qui en résultent.
1°)
C(AB) = (c1+(C2.C1/(C1+C2))) * (C2.C1/(C1+C2)) /[(c1+(C2.C1/(C1+C2))) + (C2.C1/(C1+C2))]
C(AB) = (C1²C2(C1+C2)+C2².C1²)/(C1+C2)) /[(c1(C1+C2)+C2.C1) + C2.C1]
C(AB) = (C1³C2 + C1²C2²+C2².C1²)/(C1+C2)) /[C1²+3C1C2]
C(AB) = (C1²C2 + 2C2².C1)/[(C1+3C2)(C1+C2)]
C(AB) = C1C2.(C1 + 2C2)/[(C1+3C2)(C1+C2)]
C(AB) = 2*5.(2+10)/[(2+15)(2+5)] * 10^-6
C(AB) = (120/119) * 10^-6 F
-----
2°)
Que proposes-tu ?
-----
3°)
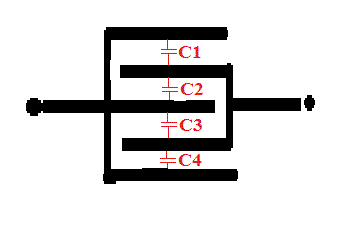
Tu peux calculer les valeurs de C1 , C2, C3 et C4 que j'ai indiqué sur le dessin.
Et puis réfléchir comment ces 4 condensateur sont interconnectés pour trouver la capacité équivalente entre les bornes repérées par des cercles noirs.
-----

Je note Cé1,2 la capacité équivalente aux 2 situés au milieu de la série des 4 Cé1,2=C1.C2/C1+C2 Donc Cé1,2 et C1 en haut sont en parallèle je note C la capacité équivalente : C=C1+Cé1,2
et en fin C1, Cé1,2 et C2 sont en série la capacité équivalente Cfinale vérifie 1/Cfinale= 1/C1+1/Cé1,2+1/C2 Voici donc le chemin que j'ai utilisé si j'ai bien compris
3°)
Pas du tout.
C1 = C2 = C3 = C4 = €o * S/d = 8,85.10^-12 * (1/2).Pi*0,03²/(0,5.10^-3) = 2,5.10^-11 F
Et ces condensateurs sont en PARALLELES pour former la capacité totale ---> C = 4 * 2,5.10^-11 = 10^-10 F = 100 pF
-----
Recopier sans comprendre est inutile, il est primordial de comprendre pourquoi C1 à C4 sont en parallèle et pas en série pour trouver la capacité entre les lames fixes et les lames mobiles.
Sauf distraction. 
Pour le 2°/ je propose ceci:
Pour 1uF:
Ceq =1/(1/C1 + 1/C2) = C1.C2/C1+C2=1uF
Ueq = U1 + U2 = 1000V
Pour 2uF
Ceq =
Ueq =
Pour 3uF
Ceq =
Ueq =
Pour 4uF
Ceq =
Ueq =
Pour 5uF
C1+C2 + C3+C4/C4+C3 =2+2+ (2+2/2+2)=5uF
Ueq = U1+U3+U4
Pour 6uF
Ceq = C1+C2+C3=2+2+2=6uF
Ueq = U1=U2
Pour 7uF
Ceq = C1+C2+C3+(C
Ueq =U1=U2
Pour 8uF
Ceq =C1+C1+C3+C4
Ueq =U1=U2
Pour 9uF
Ceq =C1+C2+C3+C4+ (C4+C5/C4.C5)
Ueq =
Pour 10uF
Ceq =C1+C2+C3+C4+C5
Ueq =
Pour 2uF et 3uF j'y réfléchis mais la question je n'arrive pas encore à la faire j'ai pas bien compris Cette question me pose vraiment d'énormes problèmes de compréhension
je veux dire la question 3°/ me pose beaucoup de problème D'abord c'est le mécanisme qui est un peu flou à mon niveau
3)
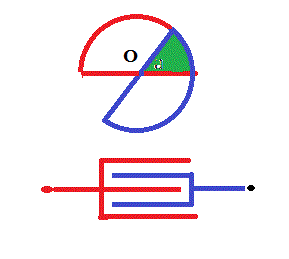
Les lames rouges sont fixes et les lames bleues peuvent pivoter autour d'un axe passant par O.
Sur le dessin, on voit que les lames fixes (qui constituent une des armatures du condensateur) et les lames bleues (qui constituent la 2eme armature du condensateur)ne se "voient" que sur le secteur que j'ai mis en vert.
En faisant pivoter les lames bleues autour de 0, on peut agrandir ou diminuer l'aire du secteur vert.
Cela fait varier la valeur de la capacité entre les lames bleues et les rouges.
La valeur max de la capacité est atteinte lorsque les lames bleues et rouges sont juste en regard l'une de l'autre. A ce moment le secteur vert est un demi cercle.
C'est la valeur de la capacité lorsque les lames bleues et rouges sont juste en regard l'une de l'autre (donc lorsque l'angle a sur ton dessin vaut 180°) qu'on te demande de calculer.



