Inscription / Connexion Nouveau Sujet
coefficient de dilatation thermique
Hello,
j'aurai besoin d'aide pour ce problème
Le Groupe intergouvernemental sur
l'évolution du climat de l'ONU prédit un
réchauffement climatique de 2 °C d'ici 2100.
Calculer l'élévation du niveau des océans
Δh, sachant le volume V0 et la surface A0
des océans du globe terrestre sont
respectivement de 1,37·109 km3 et de
361·106 km2.
voici ce que j'ai fais : alpha = delta V / delta Vo * delta T
Delta V = alpha*Vo*delta T = 207*10^6*137*10^18*275,15= 7,80*10^28m^3
mais après je ne sais pas comment trouver delta h est-ce que qqn pourrait-il m'aider ?
merci beaucoup !
bonjour,
j'ai du mal à suivre ton calcul:
par définition de 
V = Vo T
avec qui est de l'ordre de 10-4 USI pour l'eau, et T = 2 °C
de plus V = Ao h
sauf erreur
Delta V = Vo * alpha * Delta T
alpha varie avec la température ...
Il faut prendre ici alpha pour la température moyenne de la Terre, soit environ 15°C.
Voir ici : 
:
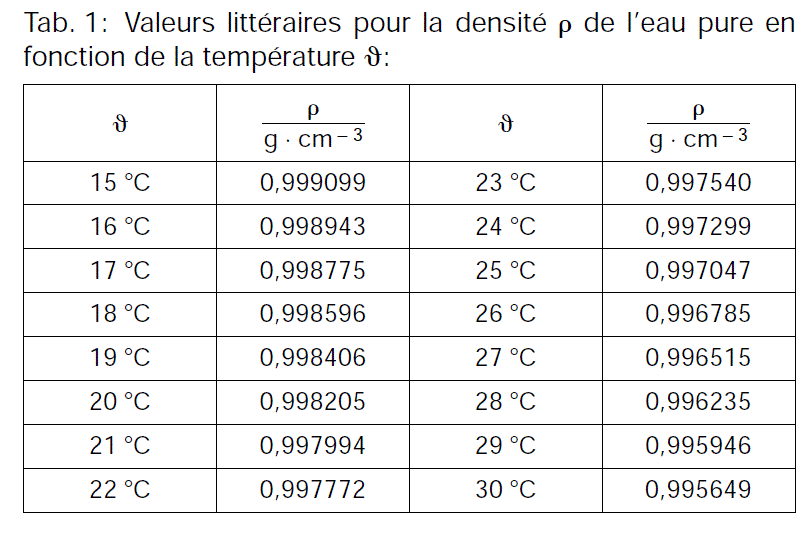
On calcule alors à 15°C : alpha = (0,999099 - 0,998943)/0,999099 = 1,56.10^-4 K^-1
(On trouve souvent dans la littérature alpha = 2,6.10^-4 K^-1, c'est une valeur valable uniquement aux alentours de 25°C ... mais ce n'est malheureusement presque jamais précisé)
Delta V = Vo * alpha * Delta T = 1,37.10^9 * 1,56.10^-4 * 2 = 4,2744.10^5 km³
Delta h = Delta V/Aire = 4,2744.10^5/(361.10^6) = 0,0012 km = 1,2 m
-----
Naturellement, on peut ergoter sur plusieurs points.
D'abord la valeur de alpha prise pour la température moyenne de l'eau introduit une erreur... par forcément négligeable.
La valeur de alpha trouvée est ici pour l'eau pure, celle de l'eau de mer est un peu différente.
...
Merci beaucoup pour toutes vos réponses, très claire et détaillée 
par contre le résultat du problème est 2,5 m ...
Le résultat est 2,5 m parce que la valeur de alpha utilisée par le "correcteur" n'est pas celle que j'ai utilisée.
J'ai expliqué comment j'avais calculé la valeur de alpha et pourquoi.
Ce n'est sans doute pas le cas du "correcteur" qui a fourni la réponse 2,5 m.
Ici :
On peut calculer alpha pour l'eau en fonction de la température à partir des courbes en fin de page 1 du lien.
Il faut évidemment prendre la courbe du bas (avec aucun glycol ajouté), et pour avoir alpha, il faut faire la dérivée. (soit mesurer les pentes des tangentes à la courbe pour les températures désirées).
On le faisant, on retrouve environ alpha = 1,56.10^-4 pour theta = 15°C.
Mais ce qu'il faut surtout voir est que la pente de la tangente à la courbe varie fort avec la température...
Et on voit aussi que la valeur de alpha qu'il faut pour trouver la réponse du corrigé, correspond à une température d'eau beaucoup trop grande.
Annuler
connectez vous