Inscription / Connexion Nouveau Sujet
Champ g.
Bonjour ,
Merci d'avance. 
Un basketteur , tire en direction
du panier constitué par un simple cercle métallique, dont le plan
horizontal est situé à 3,05 m du sol.
Lorsque le ballon est lancé par le joueur A :
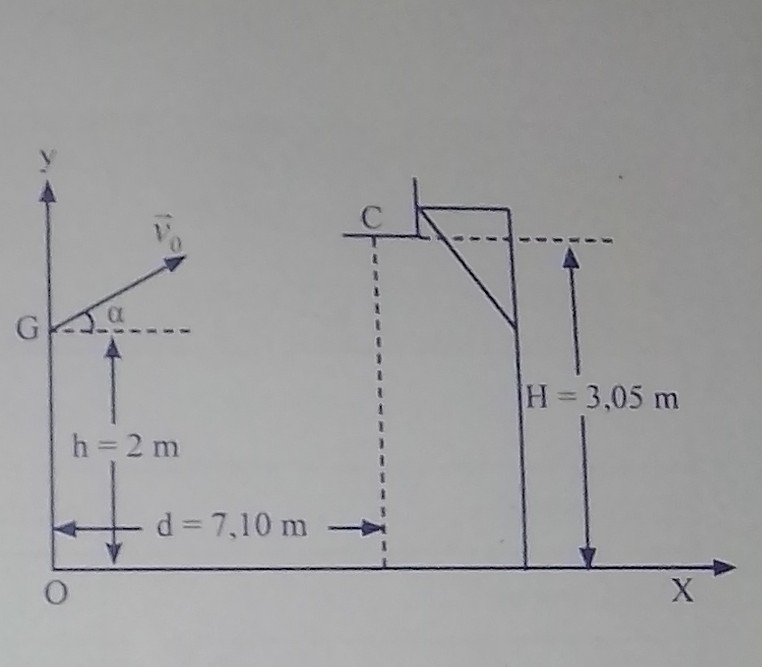
• le centre G du ballon est à 2,00 m du sol ;
• la distance séparant les verticales passant par le centre C du panier et G est 7,10 m ;
• sa vitesse , fait un angle α= 45° avec l'horizontale.
(voir figure).
Le panier est marqué ou réussi lorsque le centre du ballon passe par le centre du panier.
On néglige l'action de l'air sur le ballon.
Données numériques : Masse du ballon: m = 0,60 kg ; g =9,80 m.s²
1)
1-1) Montrer que l'équation de la trajectoire de G dans le repère (OX, OY)est avec YG=2m.
1-2) Vérifier que y peut se mettre sous la forme
2) Calculer la valeur de V0 pour que le panier soit réussi.
3) Dans la suite de l'exercice, la valeur de la vitesse du ballon au départ est V. - 9,03 m/s.
3-1) Établir et calculer la durée nécessaire au ballon pour parvenir au centre du panier.
3-2 En utilisant le theoreme de l'énergie cinétique, calcule la valeur de la vitesse du ballon lorsque le panier
est marqué.
3-3) Un joueur B de l'équipe adverse, situé à 0,90 m du joueur A, entre celui-ci et le panier, tente maintenant
d'empêcher le tir en levant verticalement les bras. La hauteur atteinte par B est 2,70 m.
Dire si le panier sera marqué , sachant que le ballon part avec la même vitesse V que précédemment.
Alors je n'y arrive pas dès la première question..
J'ai essayé de faire le schéma et représenter .
Et au niveau de la question 1-2) je ne vois pas vraiment l'intérêt de cette question.
Question 1.1
C'est une question de cours : Voir --> ![]() Mouvement d'un projectile dans le champ de pesanteur
Mouvement d'un projectile dans le champ de pesanteur
1-1) 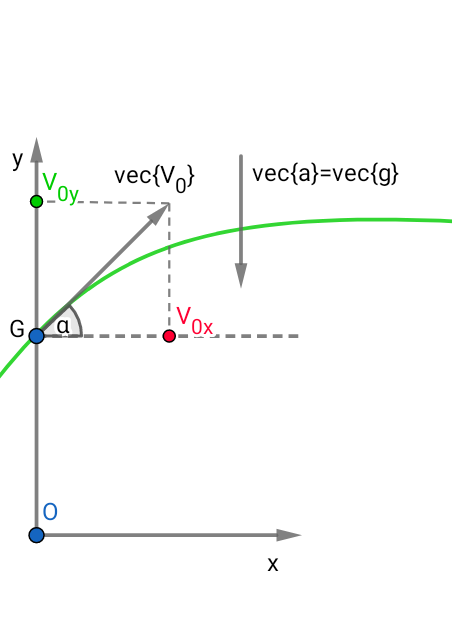
Système : La balle
Référentiel : Terrestre supposé galiléen.
Bilan des forces : Le poids .
Application du théorème du centre d'inertie.
donc le mouvement est uniformément varié.
*
*
À t=0 s ,
G(0 ; yG=h=2m)
==>
À t ≠ 0s
1-2) C'est quoi le processus pour arriver à la bonne expression ?
Question 1-1) : OK
1-2) C'est quoi le processus pour arriver à la bonne expression ?
Commencer par vérifier si tu as bien recopié l'énoncé de cette question.
Question 1-2)
D'accord !
Le but poursuivi de cette question est de simplifier au maximum l'équation établie à la question précédente afin de faciliter les calculs à venir.
3) Dans la suite de l'exercice, la valeur de la vitesse du ballon au départ est V=9,03 m/s.
et
.
et
D'où
Donc
2) On a :
Le panier est marqué lorsque la balle est au point C.
Application numérique :
,
[/tex]
Donc lorsque le panier est réussi , V0=9,03 m/s
3-1) D'après la relation (1) à la première question ,
3-2) D'après le théorème de l'énergie cinétique ,
avec
VG=V0= 9,03 m/s
3-3) Je ne vois pas vraiment..
Question 1-2)
OK
Question 2)
Mauvais départ à la ligne 1 (de cette question)
"Rattrapage" acrobatique à la ligne 3
Résultat final exact.
AN : J'ai trouvé VC = 9,0366 m/s soit après arrondi à 3 chiffres significatifs VC = 9,04m/s
Question 3-1)
OK
Question 3-2)
Erreurs de calcul à partir de la ligne 3 (de cette question)
Question 3-3) : Le panier sera marqué si le ballon passe au dessus du bras du joueur de l'équipe adverse.
Une coquille
Application numérique :
g= 9,8 N/kg
H=3,05 m
h= 2,00 m
3-3)
Application numérique :
B est situé à 0,90 m de A.
Donc xB= 0,90 m ;
le ballon part avec la même vitesse V que précédemment.
Donc VB=V0=9,03 m/s
yB=2,80 m > 2,70 m.
Donc à l'abscisse xB=0,90 m du joueur B , la balle est à une hauteur ¶ = 2,80 m.
Or la hauteur atteinte par le joueur B est 2,70 m.
Donc B l'intercepte pas la balle.
Le panier est donc réussi dans ces conditions.
Une coquille
Une coquille ? : Je ne crois pas.
Je persiste : (h - H) et non (H-h)
Application numérique :
Une coquille ?
VG = 9,03 m/s et non 0 m/s
Question 3.3 :
Ton calcul est exact, mais concerne le centre du ballon ....
Et un ballon de basket a un rayon supérieur à 10cm
Application numérique :
g= 9,8 N/kg
H=3,05 m
h= 2,00 m
Mais j'avoue que je ne comprends pas pourquoi on fait h-H et pas H-h.
Et un ballon de basket a un rayon supérieur à 10cm
Ok mais pourquoi l'énoncé ne nous le donne pas ?
Comment est-ce que ça peut intervenir dans les calculs ici ?
Mais j'avoue que je ne comprends pas pourquoi on fait h-H et pas H-h.
Tu trouveras la démonstration du calcul du travail du poids ici -->
Tu peux aussi remarquer qu'en utilisant (H-h) à la place de (h-H) tu trouverais une vitesse en C supérieure à la vitesse en G ce qui est impossible puisque le point C se situe au dessus du point G
Ok mais pourquoi l'énoncé ne nous le donne pas ?
Comment est-ce que ça peut intervenir dans les calculs ici ?
Ton calcul est exact.
Je faisais seulement remarquer que l'énoncé manquait de réalisme.
Le panier est marqué si
YB - R > YJ
YB = 2,80m (ordonnée du ballon pour x=0,9m)
R : Rayon du ballon de basket (valeur à rechercher, par exemple sur internet)
YJ = 2,70m (ordonnée de l'extrémité de la main du joueur adverse)


