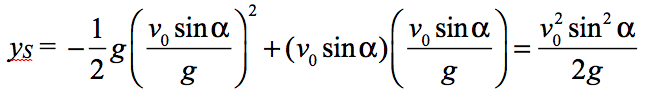Inscription / Connexion Nouveau Sujet
Calcul de la flèche
Bonsoir,
J'ai un petit soucis concernant une formule. En effet, je ne retombe pas sur le résultat souhaité malgré une multitude de calculs ...
L'image est en pièce jointe. Je ne vois pas du tout comment prendre la formule pour retomber sur le résultat. J'ai beau développer les carrés, faire attention à enlever les numérateurs quand c'est possible, rien n'y fait.
Merci d'avance pour votre aide !
Bonjour
Ton ordonnée a pour équation horaire (on prend visiblement y = 0 à t = 0)
y(t) = -1/2gt2 + v0sin t
t
L'extremum étant atteind pour vy = 0
or vy(t) = -gt + v0sin
Donc l'extremum est atteind pour ts = v0sin /g
/g
En utilisant l'expression de y(t) ci dessus, tu calcules y(ts) et du tombes pile poil sur la valeur que tu mentionnes dans ta question
Si c'est le calcul de y(t) qui te pose problème, tu pars de l'accélération: y''(t) = -g et tu intégres 2 fois...
Est ce plus clair?
Bonjour à tous les deux,
Il n'est pas impossible (j'ai rencontré cela dans un topic il y a quelque temps) que la question soit de savoir simplifier
Il suffit de mettre en facteur :

Oui... malheureusement, les bras m'en tombent souvent 
Je suis en train de rechercher ce topic, mais il est assez ancien et je ne le retrouve plus immédiatement. Mais je le retrouverai !

Un peu laborieux... 
![]() équation loi de newton
équation loi de newton
Oui, il n'est pas rare que le forum réserve des surprises.