Inscription / Connexion Nouveau Sujet
Avec la méthode d'Euler (dipôle RL)
Bonjour, nous aurions besoin de votre aide pour nous aider à réaliser un exercice type sur les dipôles RL.
La réponse en courant d'un dipôle RL à un échelon montant de tension est régie par une équation différentielle du premier ordre. Cet exercice utilise la méthode d'Euler dans le but de résoudre numériquement cette équation.
A l'instant t0 = 0s, on branche une bobine purement inductive d'inductance L = 1,0 H en série avec un conducteur ohmique de résistance R = 1,0 k aux bornes d'un générateur idéal de tension f.é.m E= 5.0 V.
aux bornes d'un générateur idéal de tension f.é.m E= 5.0 V.
1)a) Établir l'équation différentielle vérifiée par l'intensité du courant i(t) dans le circuit.
b) Donner la valeur initiale de l'intensité i(t0).
2)a) A partir de l'équation différentielle établie à la question 1)a), calculer la valeur initiale de di/dt (0).
b) La méthode d'Euler permet de calculer, pas à pas, les valeurs de i(t) et de di/dt à intervalles de temps régulier t.
D'après la définition de la dérivée, si l'intervalle de temps t est petit : i(tn + 1) = i(tn) + di/dt (tn) *  t.
t.
On choisit t = 5*10-5s. En appliquant la méthode d'Euler, compléter le tableau ci dessous :
t(*10-4s) 0 0.5 1 1.5
i(t)
di/dt
3)a) La solution de l'équation différentielle est de la forme : i(t) = A(1-e- t). Déterminer les valeurs des coefficients A et
t). Déterminer les valeurs des coefficients A et  ).
).
b) Calculer les valeurs théoriques de i(t) aux instants figurants dans le tableau précédent. Comment améliorer la précision de la méthode d'Euler ici ?
Merci d'avance de nous 5 
Bonne soirée et bon weekend tout de même 
Edit Coll : balises ! 
1)a) Établir l'équation différentielle vérifiée par l'intensité du courant i(t) dans le circuit.
b) Donner la valeur initiale de l'intensité i(t0).
2)a) A partir de l'équation différentielle établie à la question 1)a), calculer la valeur initiale de di/dt (0).
b) La méthode d'Euler permet de calculer, pas à pas, les valeurs de i(t) et de di/dt à intervalles de temps régulier t.
D'après la définition de la dérivée, si l'intervalle de temps t est petit : i(tn + 1) = i(tn) + di/dt (tn) *  t.
t.
On choisit t = 5*10-5s. En appliquant la méthode d'Euler, compléter le tableau ci dessous :
Nous somme désolé, on ne comprends pas pourquoi une partie ne s'affiche pas 
Bonjour
Je pense avoir trouvé les solutions pour la 1 a et b et la 2 a.
Alors 1a (R/L)i+(E/L)=(di/dt)
1b i(t)= 0
2a 5.0 A/S
Pour la suite, je ne trouve pas  , une petite aide serait la bienvenue svp, que je puisse comprendre
, une petite aide serait la bienvenue svp, que je puisse comprendre 
Bon Dimanche
Galaxies
Bonjour,
Question 1a : attention aux signes !
L(di/dt) + Ri = E
Question 1b : oui
i(t0) = 0 A
Question 2a :
mais le symbole de la seconde est s (s minuscule, jamais S majuscule)
Question 2b :
il suffit de calculer di/dt que tu connais par la réponse à la question 1a
Ensuite, connaissant i(t0) = 0 A
tu en déduis i(t1) avec t1 = t0 +  t
t
d'où la nouvelle valeur de di/dt
et on continue...
ce qui devrait donner quelque chose comme ceci :
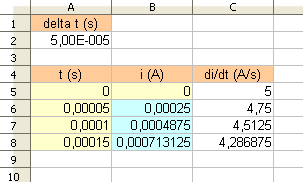
"Sauf distraction"

Merci de votre aide je vais voir si je comprends et trouve comme vous  .
.
Pour la 1 a j'ai oublié le petit "-" faute d'inattention en l'écrivant :S, merci quand même de me l'avoir fais remarqué 
Je replonge tout de suite sur la 2 b merci encore 
Merci encore pour la 2b maintenant la 3 a. je reprends un exo fais en cours et puis je verrais bien :S
L'énoncé te donne la forme de la solution i(t)
Il suffit de dériver
de remplacer dans l'équation L(di/dt) + Ri = E
et d'identifier.
Tu devrais trouver
A = E/R et  = R/L
= R/L
Ensuite pour la question 3b il suffit d'ajouter une colonne dans le tableur :
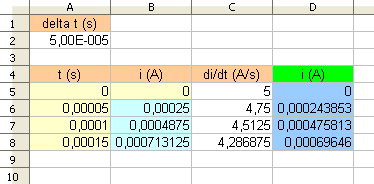
Comment améliorer la précision ? Je te laisse réfléchir.



