Inscription / Connexion Nouveau Sujet
Arrêt d'un véhicule en côte
Bonjour, j'aimerais avoir de l'aide sur cette exercice. Merci d'avance.
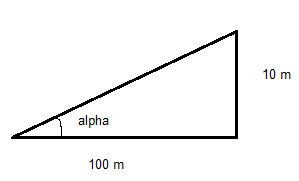
Un véhicule, freins bloqués, est immobilisé sur une route en pente de déclivité 10% (la route s'élève de 10 m lorsqu'on parcourt 100 m). La masse du véhicule est de 1,5 t.
1.Déterminer le poids du véhicule (on prendra g=10 N/kg).
2. Si 
est l'angle que fait la route avec le plan horizontale, montrer que sin=0.1.
3.a. Montrer que la force de frottement a pour valeur f=m.g.sin
b. Calculer f.
1. P=mg=1500*10=15000N
2. sin = 10/100 = 0.1
3. a.
b. f=1500*10*0.1=1500 N
Bonsoir,
C'est du "style télégraphique" mais c'est bon.
Que proposes-tu pour la question 3a ?
Référentiel ?
Repère ?
Bilan des forces ?
Loi de Newton à appliquer ?
Quel système d'axes (repère) utilises-tu ?
Quelle est la loi de Newton qui est applicable et pourquoi ?
xy... bien sûr !
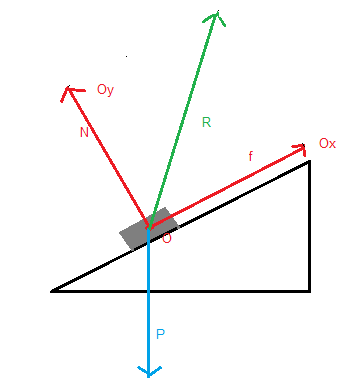
O : origine du repère au centre de gravité du mobile (le véhicule)
Ox : parallèle à la route, orienté vers le haut de la pente, par exemple
Oy : perpendiculaire à la route, donc orienté vers le haut
Comptes-tu les forces de frottement dans la réaction du support ?
Pourquoi la somme des vecteurs est-elle nulle ?
Il faut que tu cherches quelle est la loi de Newton qui s'applique.
Tu dois projeter l'égalité vectorielle sur les axes. Un dessin serait une grande aide...
1) Écris l'égalité vectorielle
2) Projette cette égalité vectorielle sur les axes.
Tu dois justifier l'égalité vectorielle.
Tu avais écrit que la somme de tous les vecteurs est nulle (ce qui reste à justifier ! )
Donc cette égalité ne convient pas.
Il faut vraiment que tu recherches du côté des lois de Newton (c'était à ton programme l'année dernière et c'est à nouveau à ton programme cette année...)
La lois sur le principe d'inertie ?
Si le centre d'inertie est au repos ou en mouvement rectiligne uniforme alors la somme des forces qui s'exercent sur le solide est nulle.
Exact.
L'énoncé dit que le véhicule est "immobilisé".
Le référentiel terrestre étant assimilé à un référentiel galiléen, la première loi de Newton s'applique (on l'appelle aussi principe d'inertie ; ce principe a été énoncé par Galilée et repris dans son ensemble de trois lois par Newton comme première loi. Newton ayant, en scientifique honnête, reconnu que ce principe avait été énoncé avant lui par Galilée).
Alors, quelle est la somme (vectorielle) des forces qui est nulle ?
Exact !
Ce qui correspond chez moi à cette figure :
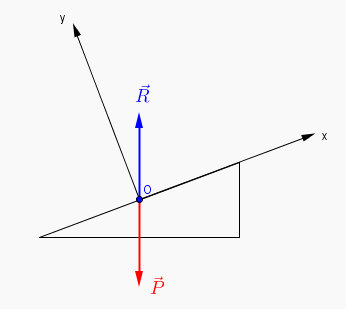
et donc l'égalité vectorielle à projeter est
Un peu de réflexion conduit à ne s'intéresser qu'à la projection sur l'axe Ox
Exact !
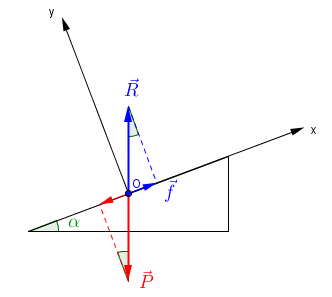
Le reste ne devrait plus présenter de difficulté.
Je ne pourrai pas te répondre tout de suite, mais je regarderai ce soir.
Ceci est vrai, mais ce qui est plus utile c'est
Si on note g le module de l'accélération due à la pesanteur, donc par exemple g = 10 N/kg
alors
avec P le module du poids, P = m.g
Mais il faut prendre les composantes des vecteurs sur les axes qui définissent le repère (au moins sur l'axe Ox)
f, force de frottement, est égale et opposée à la projection du poids sur l'axe parallèle à la route (l'axe Ox).
11 h 12 : "... tu dois projeter..."
11 h 54 : "... projette cette égalité vectorielle..."
13 h 31 : "... l'égalité vectorielle à projeter..."
16 h 43 : "... les composantes des vecteurs..."
18 h 14 : "... la projection du poids..."
La composante du vecteur sur l'axe Ox est en effet égale à
Mais... à quoi est égale cette composante ? ? ?
Que vaut la projection du vecteur sur l'axe Ox
Si cela t'amuse, tu peux aussi calculer la projection de ce même vecteur "poids" sur l'axe Oy ; mais cela ne servira à rien.
Projeter un vecteur sur deux axes perpendiculaires : programme de seconde !
Complètement faux...
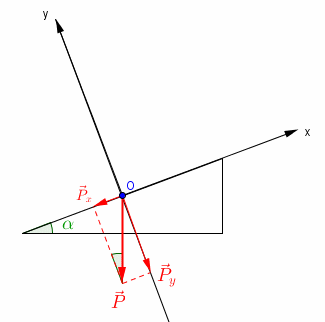
Que valent les composantes (les projections) et
du vecteur
sur les axes Ox et Oy ?
Annuler
connectez vous