Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Niveau terminale
Partager :

Accélération et décélération.

Posté par
kamikaz 05-12-20 à 19:10

Bonsoir ,

Merci d'avance.

Au cours d'activité sportive en athlétisme , deux amis Pierre et Jean effectuent l'épreuve de 100 m qui consiste à parcourir une distance de 100 m en ligne droite.
La piste est munie du repère d'espace (O , \vec{i}) et la position d'un coureur à la date t est repérée par le point M par projection sur l'axe (O ,\vec{i}) .
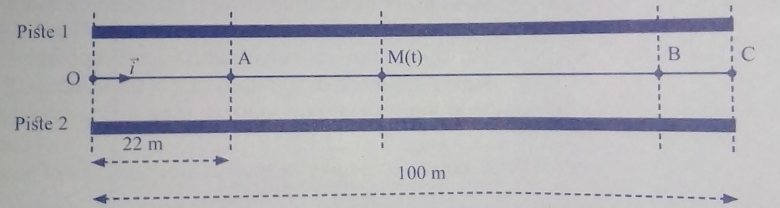
Les deux démarrent sur la même ligne d'abscisse x0=0 , à la date t0 origine du repère de temps. Leurs mouvements sont uniformément accélérés et de la même façon , de sorte qu'elles parcourent la même distance OA=22 m entre les dates t0 et t1=6 s . À partir de là distance OA , Pierre accélère davantage et franchit la ligne d'arrivée repérée par le point B , d'où elle ralentit progressivement pour s'arrêter après avoir parcouru la distance BC=10 m (voir schéma ci-dessous).

Accélération et décélération.

Le chronomètre marque comme durées de parcours des 100 m : 12 s pour Pierre et 13 s pour Jean.

On désire évaluer les vitesses et accélération des deux athlètes.

1) Donner les équations horaires d'un mobile M animé d'un mouvement rectiligne uniformément varié dans un repère (O ,\vec{i}) , en fonction de son accélération a et de vitesse V0.

2) Déterminer à l'issue de la première phase du trajet :

2-1) L'accélération des coureurs ;

2-2) La vitesse des coureurs.

3) Déterminer :

3-1) L'accélération de chaque coureur sur la deuxième phase de son mouvement ;

3-2) La vitesse avec laquelle Pierre franchit la ligne d'arrivée.

4) Déduire de la question précédente , la décélération du mouvement de Pierre lorsqu'il ralentit progressivement après la ligne d'arrivée pour s'arrêter.

Réponses

1) L'équation horaires est du mobile M est : X(t)=\dfrac{1}{2}at²+V_{0}t+x_{0}

2-1) Ils démarrent sur la même ligne d'abscisse x_{0}=0 m à la date t0 origine du temps.

Donc V0=0 m/s

Donc X(t)=\dfrac{1}{2}at².

Durant la première phase , ils parcourent OA = 22 m.

Donc X = 22 m

22=\dfrac{1}{2}a(t_{f}-t_{0})²

tf=6 s et t0=0 s

22=\dfrac{1}{2}×a×6²

a=1,22 m/s²

Donc l'accélération de Pierre et Jean est a= 1,22 m/s².

2-2) On sait que V(t)= X'(t)

Donc V(t)= a(t_{f}-t_{0})

V= 1,22×6= 7,33 m/s

La vitesse de Pierre et Jean est V= 7,33 m/s.


3-1) Pour Jean , on a ;

X_{f}(t)=\dfrac{1}{2}×a(t_{F}-t_{6})²

tF : le temps finale = 13 s.

X(t)= \dfrac{1}{2}×a×(13-6)²

X_{f}(t)=\dfrac{1}{2}×a×7²

Xf= 100 -22= 78 m

Donc 78=\dfrac{1}{2}a×7²

a=3,18 m/s²

Donc V_{F}=a×7 =3,18×7=22,29 m/s

*Pour Pierre

X_{f1}(t)=\dfrac{1}{2}a(t_{F1}-t_{6})=\dfrac{1}{2}×a×(12-6)²=\dfrac{1}{2}×a×6²

X_{f1}(t)=\dfrac{1}{2}×a×6²

X=100-22 = 78

Donc 78=\dfrac{1}{2}×a×6² \iff a=4,33 m/s²

4) Soit a1=4,33 m/s² et a0=1,22 m/s²

La décélération a'=a0-a1=1,22-4,33=-3,11 m/s²

a'=-3,11 m/s²

Posté par
gts2re : Accélération et décélération. 05-12-20 à 20:07

Bonjour,

Pour le 4) je ne vois pas trop le rapport entre votre réponse et la question :
"lorsqu'il ralentit progressivement après la ligne d'arrivée pour s'arrêter."
Donc on s'intéresse à ce qui se passe entre B et C.

Posté par
kamikazre : Accélération et décélération. 05-12-20 à 20:15

Et pour mes réponses autres questions ?

Posté par
gts2re : Accélération et décélération. 05-12-20 à 20:21

Pour le reste, cela a l'air de tenir la route.

Posté par
kamikazre : Accélération et décélération. 05-12-20 à 20:36

Citation :
Donc on s'intéresse à ce qui se passe entre B et C.


D'accord , mais on ne connait pas la longueur BC , je fais comment ?

Posté par
gts2re : Accélération et décélération. 05-12-20 à 20:49

Citation du texte : "après avoir parcouru la distance BC=10 m"

Posté par
kamikazre : Accélération et décélération. 05-12-20 à 20:51

Ah oui , donc je calcule l'accélération entre B et C non ?

Posté par
gts2re : Accélération et décélération. 05-12-20 à 22:36

Oui, c'est bien cela.

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 14:41

Une petite question , à la question 1) , l'énoncé demande de donner les équations horaires.

Mais j'ai trouvé qu'une seule..

Est-ce qu'il y en a d'autres ?

4) On a : l'équation horaire X(t)' de Pierre entre B et C est :

X(t)'=\dfrac{1}{2}a't_{B}²

a' : la décélération recherchée

tB = 12 s

X= BC = 10 m

Donc 10=\dfrac{1}{2}a'×12²

a'=0,14 m/s²

Donc la décélération de Pierre après la ligne d'arrivée est a'= 0,14 m/s²

Posté par
gts2re : Accélération et décélération. 06-12-20 à 14:46

Pour 1) je ne vois pas.
Pour 4) Incohérent vous utilisez tB qui est le temps pour aller de O à B pour étudier ce qui se passe entre B et C.
D'autre part, en B la vitesse n'est pas nulle.
Vous donner X(t) avec la variable t je suppose et vous donnez comme expression de cette fonction une constante.

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 15:04

Citation :

1) Donner les équations horaires d'un mobile M animé d'un mouvement rectiligne uniformément varié dans un repère (O ,\vec{i}) , en fonction de son accélération a et de vitesse V0.



4) On a : l'équation horaire X(t)' de Pierre entre B et C est :

X(t)'=\dfrac{1}{2}a't_{f}²

a' : la décélération recherchée

tf'=  12-6 = 6s

X= BC = 10 m

Donc 10=\dfrac{1}{2}a'×(12-6)²

a'=0,55 m/s²

Donc la décélération de Pierre après la ligne d'arrivée est a'= 0,55 m/s²

Posté par
gts2re : Accélération et décélération. 06-12-20 à 15:10

Votre équation horaire n'est pas une équation horaire, puisque ne dépendant pas de t.
Je répète : "en B la vitesse n'est pas nulle"
12 s c'est entre O et B ;  6 s entre  O et A. On étudie entre B et C.

Autrement dit, avant d'écrire quelques équations que ce soit, que pouvez-vous dire de (décrivez) ce qui se passe entre B et C ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 15:17

Il y a une décélération entre B et C.

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 15:28

Citation :
Votre équation horaire n'est pas une équation horaire, puisque ne dépendant pas de t.


Donc je fais comment pour la première question ?

Posté par
gts2re : Accélération et décélération. 06-12-20 à 15:39

Citation :
Donc je fais comment pour la première question ?


On en est à la quatrième !

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 15:59

Mais je crains que ce soit  faux..

Je fais comment pour la 4e question ?

Posté par
gts2re : Accélération et décélération. 06-12-20 à 16:03

Pour la 1, c'est parfaitement juste, peut-être un problème de rédaction mais cela dépend de votre cours.

Pour la 4), il faut commencer par décrire en français ce qui se passe entre B et C : que saiton en B ? que sait-on en C ? que se passe-t-il entre les deux ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 16:16

On est à la position B à t= 12 s avec une vitesse V= 25,98 m/s et une accélération a = 4,33 m/s²

On est en C avec à une date t qu'on ne connait pas vraiment et avec une vitesse V = 0 m/s.

Entre B et C , Pierre diminue donc sa vitesse acquise au point B et s'arrête en C.

Posté par
gts2re : Accélération et décélération. 06-12-20 à 16:32

Ce n'est pas mis clairement dans le texte, mais on peut supposer que le mouvement est uniformément varié.

Donc comment s'écrit l'équation horaire du mouvement entre B et C (vous avez intérêt à prendre l'origine des temps et d'espace en C) ?
Comment s'écrit v(t) entre B et C ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 16:39

V(t)= at+ Vb ( Vb la vitesse en B)

Posté par
gts2re : Accélération et décélération. 06-12-20 à 16:58

Oui et donc ...

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 17:04

Donc V= a ×12 + 25 , 98

Or V= D/t ==> V = 10/13 =0,77 m/s

Donc 0,77 = 12a +25,98

12a= -25,21

a=-2,10 m/s²

Posté par
gts2re : Accélération et décélération. 06-12-20 à 17:15

Le mouvement n'est pas uniforme donc V\neq D/t

V(t) par définition (sauf cas particulier de mouvement uniforme) dépend de t, donc cela ne peut être une constante

Traduisez ce que vous avez écrit :

Citation :
On est à la position B à t= 12 s avec une vitesse V= 25,98 m/s.

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 17:34

Pourtant c'est ce que je croyais faire en écrivant Vb = 25,98 m/s

Posté par
gts2re : Accélération et décélération. 06-12-20 à 17:36

Vb=25,98m/s est la vitesse à l'instant t'=0 (nouvelle origine des temps pour se simplifier un peu la vie).
Le mouvement est uniformément varié, que vaut V(t') ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 17:38

V(t')= a t' +Vo

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 17:39

Mais ici Vo = Vb=25,98 m/s  non ?

Posté par
gts2re : Accélération et décélération. 06-12-20 à 17:40

C'est bien V(t')= a t' +Vo avec Vo = 25,98 m/s

On passe on point C, que vaut v ? et donc que peut-on en déduire ?

Etape suivante x(t')= ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 19:50

Au point C , la vitesse V= 0 m/s car il s'arrête.

x(t')= 1/2 at'² +Vot' + xo

Posté par
gts2re : Accélération et décélération. 06-12-20 à 19:55

On y est presque.
Simplifiez vous la vie en prenant l'origine en B.
Il s'arr^te donc t'(arrêt)= ?
et donc x(t'(arrêt))= ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 19:59

t'(arrêt)= 0 s.

et donc x(t'(arrêt))= 1/2 at'(arrêt)² +Vot'(arrêt)+ xo

Posté par
gts2re : Accélération et décélération. 06-12-20 à 20:01

Si on s'arrête, cela veut dire quoi sur la vitesse ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 20:06

Oups

V = D/t

Donc t=D/V

t= 10 / 25,98 = 0,38

Donc t entre B et C est 0,38 s

D'où t'(arrêt) = 12 s + 0,38 s = 12,38 s

et donc x(t'(arrêt))= 1/2 at'(arrêt)² +Vot'(arrêt)+ xo

x(t'(arrêt))= (1/2)×a×12,38²+25,98×12,38

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 20:07

gts2 @ 06-12-2020 à 20:01

Si on s'arrête, cela veut dire quoi sur la vitesse ?


La vitesse est nulle.

Posté par
gts2re : Accélération et décélération. 06-12-20 à 20:11

Citation :
V = D/t


Combien de fois faudra-il répété que cela ne concerne qu'un mouvement uniforme et qu'ici on freine.

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 20:12

Ah oui , désolé

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 20:14

Dans ce cas comment trouver t'(arrêt) ?

Posté par
gts2re : Accélération et décélération. 06-12-20 à 20:23

Vous avez écrit :

Citation :
V(t')= a t' +Vo
Vo = 25,98 m/s
Au point C , la vitesse vaut V= 0 m/s

Et donc ?

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 20:28

Donc at'+ 25,98 = 0

Posté par
gts2re : Accélération et décélération. 06-12-20 à 20:31

C'est bien cela.

Il reste à utiliser la distance BC grâce à x(t').

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 20:33

Comment utiliser x(t') dans at'+25,98= 0 ?

Posté par
gts2re : Accélération et décélération. 06-12-20 à 20:45

Il ne s'agit pas d'utiliser x(t') dans ...

mais d'utiliser les deux équations
at'(arrêt)+25,98= 0
et
x(t'(arrêt))=1/2 at'(arrêt)² +Vo t'(arrêt)+ xo

pour trouver a.

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 20:57

Ah d'accord , donc le système à résoudre : \begin{cases} at'_{arret}+25,98=0 \\ xt'_{arret}=\dfrac{1}{2}at'_{arret}²+V_{0}t'_{arret}+x_{0} \end{cases}

On a xo=BC=10 m , mais on ne connait pas t'(arrêt)

Posté par
gts2re : Accélération et décélération. 06-12-20 à 21:04

Il se peut que n'ayez pas encore vu cela en maths, mais ici vous avez deux équations (vitesse nulle d'un côté, distance BC de l'autre) et deux inconnues a et t', donc on peut y arriver.
Le plus simple est de calculer t' dans la première (la vitesse), sous forme littérale (c'est plus pratique) et de reporter ce t' dans x(t'), vous aurez bien alors une équation avec une inconnue a.  
Il y a des méthodes plus directes, mais on garde ici dans les raisonnements précédents.

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 21:09

Ah oui , effectivement

Posté par
kamikazre : Accélération et décélération. 06-12-20 à 21:12

x = BC = 10 m

Ou bien xo = BC = 10 m ?

Posté par
gts2re : Accélération et décélération. 06-12-20 à 22:43

Le plus simple est de prendre l'origine en B (x=0,t=0), donc x0=0 et x(t'(arret))=BC=10m.

Faites le calcul littéral, vous reconnaitrez peut-être la méthode directe.

Posté par
kamikazre : Accélération et décélération. 07-12-20 à 00:47

Je sais faire , mais je confondais xo et x..

Posté par
kamikazre : Accélération et décélération. 07-12-20 à 15:28

Bonjour ,

Si on simplifie l'écriture du système :

\begin{cases} at'+25,98=0 \\ xt'=\dfrac{1}{2}at'²+V_{0}t'+x_{0} \end{cases} \\

\begin{cases} at'=-25,98 \\ 100t'=\dfrac{1}{2}at'²+10 \end{cases} car x = 100 m , xo = 10 m et Vo = 0 m/s.

\begin{cases} at'=-25,98 \\ 100t'=\dfrac{1}{2}(-25,98)²+10 \end{cases}

\begin{cases} at'=-25,98 \\ t'=\dfrac{\dfrac{1}{2}(-25,98)²+10}{100} \end{cases}

\begin{cases} at'=-25,98 \\ t'=4,374802 s \end{cases}

\begin{cases} a×4,374802=-25,98 \\ t'=4,374802 s \end{cases}

\begin{cases} a=-5,94 m/s² \\ t'=4,374802 s \end{cases}

Donc la entre B et C est : a= -5,94 m/s²

D'où la décélération de Pierre après avoir franchit la ligne d'arrivée est a=-5,94 m/s².

Posté par
gts2re : Accélération et décélération. 07-12-20 à 15:51

Bonjour,

De grâce, faites des calculs littéraux.

\begin{cases} at'+V_0=0 \\ \dfrac 12 at'^2+V_0t'=BC \end{cases} \\  
On a dit qu'on se simplifiait la vie en prenant l'origine en B. Le t' ci-dessus est l'instant d'arrivée en C.

Deuxième équation, sacré méli-mélo
- entre x(t') et x*t' ;
- entre 10 qui est la valeur finale et x0 la  valeur initiale ;
- entre 100 qui est la valeur initiale et x(t') qui est la valeur finale ;
- entre 100 avec origine en A et 10 avec origine en B ...

Equation 3 vous remplacez a*t2 par (at)2

Equation non homogène : cela ne se voit pas parce que vous faites des calculs numériques
....

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !