Inscription / Connexion Nouveau Sujet
2ème système quantique
Un électron, dont le hamiltonien ne dépend pas du temps, est dans l'état quantique décrit par la fonction d'onde ψ(x,t)=c0.(x)e^(−iE0.t/)+c1.φ1(x)e^(−iE1t/
) où E0≠E1 et φ0(x) et φ1(x) sont les fonctions propres du hamiltonien pour les valeurs propres E0 et E1, respectivement.
Est-ce que la densité de probabilité de présence dans l'espace de l'électron est stationnaire ?
La densité de probabilité cherchée est
En développant (sauf erreur), je trouve l'intégrale entre - et +
et + de |c0|²|φ0|² + |c1|²|φ1|² ???
de |c0|²|φ0|² + |c1|²|φ1|² ???
A priori ça semble indépendant du temps, mais je ne suis pas convaincu ???
Merci pour ta réponse!
J'ai coché "oui" sur la réponse au QCM et malheureusement ce n'est pas la bonne réponse ...
Restent "Non" ou "Cela dépend de la forme des fonctions φ0(x) et φ1(x)" ???
Bonsoir!
En fait, la densité de probabilité de présence dans l'espace de l'électron est donnée par le module carré de la fonction d'onde ∣ψ(x,t∣² (supposée normalisée=. Dans le calcul (que j'ai refait en PJ)
Il apparaît 2 termes dépendants de t car on considère 2 niveaux d'énergie distinctes E0 et E1. Donc la densité de probabilité de présence dans l'espace de l'électron est modifiée au cours du temps !
(pour que la densité de présence soit stationnaire, il eu fallu que E0=E1)
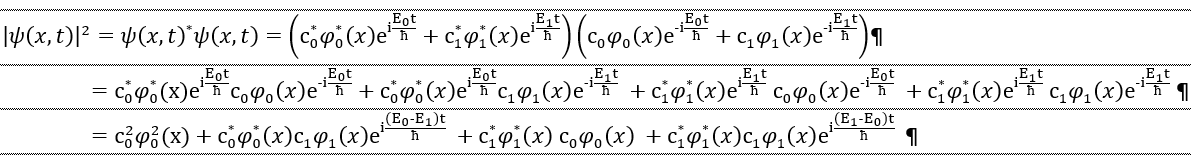


 en post-bac
en post-bac