Bonjour jolechti56,

tu as fait le plus difficile en écrivant m + m' = 0. Cette relation devient m = -m' soit = -(m'/m). On en déduit que :
a)   les vecteurs et sont colinéaires (même direction) puisque la relation est du type = K. ;
b)   ces deux vecteurs sont de sens contraire car la constante K est négative :
c)   leurs normes sont liées par la relation v = K.v', et comme K vaut m'/m = 1/100, la norme de est cent fois plus petite que celle de , soit 4 m.s^-1.

En définitive : le vecteur-vitesse du canon est dirigé en sens contraire de celui du boulet, et sa norme est divisée par cent.  OK ?

Ok c'est très clair merci

Juste un autre truc, j'arrive jamais à savoir si un système est isolé, pseudo-isolé ou rien du tout.

Je sais ce que ces termes signifient mais j'ai du mal à les exploiter sur un exercice. Là par exemple le système canon,boulet il est isolé ou pseudo-isolé ?

En physique, on appelle système un ensemble d'objets (deux au minimum) quelconques, donc pouvant être solides, liquides ou gazeux. Tous les autres objets qui n'appartiennent pas à ce système constituent l'environnement extérieur. Quelques exemples : a) la Terre et la Lune, l'environnement extérieur étant le Soleil, les autres planètes et leurs satellites, les autres étoiles et galaxies ; b) le Soleil et les planètes du système solaire, l'environnement étant les autres étoiles de notre galaxie ; une molécule d'un liquide ou gaz donné, l'environnement étant constitué de toutes les molécules qui entourent celle qu'on étudie ; d) les molécules d'un liquide contenu dans un récipient, l'environnement étant la pièce où se trouve ce récipient, l'étagère sur laquelle il est rangé, et la Terre en général. Comme tu le vois, les situations que l'on rencontre en faisant cette distinction système - environnement sont innombrables.

En mécanique, on dit qu'un système est isolé s'il n'est soumis à aucune force de la part de son environnement. On dit qu'un système est pseudo-isolé s'il est soumis de la part de son environnement à plusieurs forces dont la résultante (càd la somme) est nulle.

Réaliser un système isolé est quasi impossible : il faut éviter toute contrainte mécanique (liaisons avec câbles ou ressorts reliant ce système à l'environnement extérieur, support sur lequel ce système serait posé), mais aussi : pas de champ électrique ou magnétique, et surtout pas d'influence de la pesanteur terrestre ou du champ de gravitation d'un autre astre. Il n'y a guère que dans le vide sidéral, loin du Soleil, de la Terre et de toute autre étoile, que l'on peut envisager un tel système. Un grand moment de solitude...

En revanche un système pseudo-isolé est bien plus fréquent : il s'agit simplement d'énumérer les forces qui s'appliquent dessus, issues du reste de l'univers, et de vérifier que leur somme vectorielle (càd leur résultante) est nulle.
Exemple issu de cet exercice : le canon et son boulet (idem : arc et flèche, fusil et balle etc...). Lorsque le boulet est encore dans le canon et que l'ensemble est posé sur un sol parfaitement horizontal, le poids canon + boulet est compensé par la réaction du sol ; si de plus on néglige la résistance de l'air sur le boulet qui avance et le fût du canon qui recule, alors le système canon + boulet est pseudo-isolé et on peut appliquer la conservation de la quantité de mouvement. Cet état durera tant que le boulet n'est pas sorti du canon : en effet, ultérieurement le poids du boulet n'est plus compensé par la réaction du canon, et le boulet redeviendra soumis à son poids qui est une force extérieure (càd créée par le champ de pesanteur terrestre, donc issue de l'environnement) ; la nature pseudo-isolée du système cesse dès que le boulet est arrivé à l'air libre. Dans ce cas de figure, la conservation de la quantité de mouvement ne permet donc de calculer que la vitesse avec laquelle le boulet sort du canon, ou, si on connaît celle-ci, la vitesse avec laquelle le canon recule. OK ?

Voici un petit exercice amusant qui te permettra de vérifier si tu as bien compris :

Deux barques, A et B, sont immobiles sur un lac parfaitement calme. Dans chaque barque il y a un pêcheur, et les poids des barques + leur pêcheur sont exactement les mêmes. Les deux barques sont reliées par un câble dont la longueur initiale vaut L = 10 m. A un signal donné, le pêcheur de la barque A actionne le treuil qui permet de rembobiner le câble pour rapprocher les deux barques, tandis que le pêcheur de la barque B ne fait rien. La question est : lorsque les deux barques vont se rejoindre, leur point de contact sera situé :
a) au milieu de leur éloignement initial, donc à L/2 = 5 m ; b) avant ce point puisque seul le pêcheur A actionne son treuil ; c) au contraire, plus près de la position initiale de B que de celle de A.

La réponse demain...

BB.

Très sympa de prendre le temps d'expliquer

Pour la notion de système je pense avoir compris sauf pour un exemple que j'ai rencontré dans un exercice : une fusée qui décolle. On a considéré la force de propulsion comme une force extérieure. Or c'est la fusée qui est la "source" de cette force non ? Les réacteurs appartiennent au système fusée logiquement...

Sur les systèmes pseudo-isolés y'a un petit truc que je comprends pas c'est cette phrase : "si de plus on néglige la résistance de l'air sur le boulet qui avance et le fût du canon qui recule, alors le système canon + boulet est pseudo-isolé"
Si on considère le boulet encore dans le canon, il n'y a pas à négliger son mouvement puisque justement il ne bouge pas non ?

C'est compliqué la question des deux barques

Je dirais que si on considère le système (A;B;treuil) on peut dire qu'il est pseudo-isolé. Donc la qté de mouvement se conserve. Elle est nulle au départ.
Après action du treuil, que l'on considère comme force interne, on a donc m.a=-mb
Comme les deux ont la même masse, on a a=-b

Je dirais donc la réponse a)

Bonjour jolechti56,

j'admire sincèrement la pertinence de tes questions, qui montre que tu prends le temps de réfléchir avant de les poser ; sur les 5000 étudiants (environ) que j'ai vus passer durant ma carrière, j'en ai trouvé très peu qui réagissaient comme toi. Sincèrement ! Alors voici mes réponses :

1) Je commence par ta question concernant boulet de canon, car elle me montre que je me suis mal expliqué :
On considère le système canon + boulet, rien de plus (en abrégé : B+C). L'environnement est donc : la Terre et l'atmosphère.

a)  Avant la mise à feu, canon et boulet sont immobiles. Les forces qui leur sont appliquées et qui viennent de l'extérieur sont : leur poids, et la réaction du sol. Jusque là tu as raison, il n'y a pas de frottement dû à l'air. Si le sol est parfaitement horizontal, poids et réaction se compensent, donc la résultante des forces extérieures (je reviendrai plus bas sur cette notion) appliquées au système est nulle : le système est pseudo-isolé, et l'expérience commence avec une quantité de mouvement nulle.

b)  On déclenche la mise à feu : le boulet va se mettre en mouvement mais je considère le laps de temps où il est encore dans le canon : en plus des deux forces précédentes, il y a la résistance de l'air provoquée par le déplacement du boulet (on est tout de même à une vitesse de 400 m/s, donc supérieure à la vitesse du son... l'hypothèse de la résistance de l'air est loin d'être idiote). Si on tient compte de cette force, alors le système B+C n'est plus isolé puis qu'il subit une force issue de son environnement. On ne peut donc pas dans ce cas appliquer la conservation de p... et ton exercice s'arrête là.
Si on "oublie" cette force dans un but de simplification, alors tant que le boulet est encore dans le canon la résultante des forces extérieures est nulle : on peut appliquer la conservation de p et en déduire le rapport des vitesses (celle du boulet et la vitesse de recul du canon), et calculer l'une si on connaît l'autre.
Bien entendu, dès que le boulet sort du canon, son poids n'est plus compensé par la réaction du fût : le boulet est alors soumis au champ de pesanteur et va suivre une trajectoire parabolique. D'ailleurs la notion même de système ne s'applique plus, puisque le système B+C est "cassé".

Voici une expérience amusante simulant le système B+C, tournée ici à Lille : .


2) Le problème de la fusée est sans contexte le plus ardu pour un élève de terminale, quoi qu'en pensent les rédacteurs de manuels qui l'ont mis en bonne place dans leurs bouquins... Il faut distinguer deux cas de figure : la fusée au décollage et la fusée dans le vide interstellaire.

a)  fusée au décollage : tout dépend du choix du système envisagé.
Si on prend la système la fusée + les gaz éjectés (F+G), alors juste après le décollage ce système est soumis à l'attraction terrestre qui est une force extérieure : (F+G) n'est pas pseudo-isolé).
Si on y inclut la Terre (F+G+T), alors ce système complexe devient isolé puisque l'attraction gravitationnelle y est incluse, toujours en négligeant la résistance de l'air sur la fusée comme dans le cas de (C+B). D'ailleurs les deux problèmes sont quasi-identiques, et si on te donne la vitesse acquise par la fusée juste après le décollage, tu peux calculer la vitesse de recul de la Terre (rassure-toi, elle est négligeable).

b)  fusée dans le vide interstellaire :
A priori ce cas semble plus simple puisqu'il n'y a plus d'environnement susceptible d'interagir avec la fusée. Mais là encore il faut faire attention au choix du système :
Si on prend comme système la fusée seule, celle-ci perd de la masse à cause de la combustion du carburant. Les gaz éjectés passent dans l'environnement : la fusée seule n'est pas un système isolé.
Si on prend comme système l'ensemble (F+G), cette fois les gaz éjectés font toujours partie du système : la  masse perdue par la fusée se retrouve dans celle des gaz éjectés (sous réserve que la combustion du carburant s'est faite sans perte de masse, ce qui reste à prouver...). On peut donc appliquer au système F+G la conservation de la quantité de mouvement, mais du fait du transfert de masse d'un élément du système vers l'autre la mise en équation est délicate (hors programme en TS, c'est plutôt du niveau classes prépa).

En conclusion sur ce point, pour reprendre la question posée dans ton dernier post : ce n'est pas la fusée qui est la source de la force de propulsion (facile à comprendre : si c'était le cas, la fusée dans le vide ne pourrait pas se déplacer). C'est le gaz éjecté par la combustion du carburant qui génère cette force. La fusée ira d'autant plus vite que la vitesse d'éjection des gaz est élevée.  OK ?


3) enfin, l'expérience des deux barques :
rien à dire, tu as raison elle vont acquérir la même vitesse puisque les deux masses identiques se simplifient, et donc se rencontrer après que chacune ait parcouru la même distance.

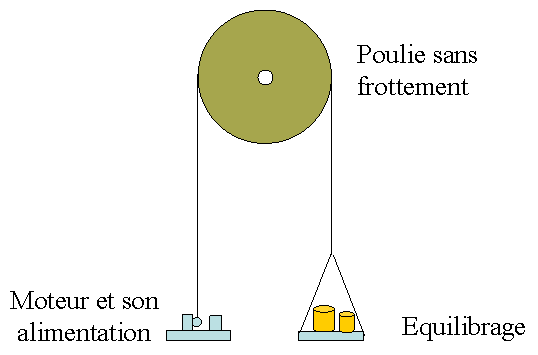
Cette expérience n'est pas facile à réaliser pratiquement, mais en voici une autre, analogue mais plus simple : il faut un fil inextensible, une poulie sans frottement, un petit moteur et son alimentation et quelques masses marquées. Avec un jeu de construction (meccano ou lego) on doit pouvoir trouver tout ça. le schéma ci-dessous montre ce qu'il faut réaliser. Quand on met le moteur en route pour rembobiner le fil, les deux plateaux montent à la même vitesse et atteignent la poulie en même temps. C'est l'analogue de l'expérience des deux barques, dans un plan vertical.

J'aurais bien aimé avoir d'autres questions à poser car vos réponses sont très claires et détaillées mais là je crois avoir vraiment tout compris

Merci beaucoup !

Bah, si d'autres questions te viennent, dans les jours ou les semaines qui viennent, ne te gêne surtout pas ! Je trouverai toujours quelques instants pour te répondre. Pour être sûr de me joindre, tu peux utiliser mon adresse mel (voir mon profil en cliquant sur le personnage à gauche de mon pseudo).

Je n'ai pas trop le temps là maintenant, mais dans quelques jours je t'enverrai la mise en équation du système fusée + gaz dans le vide. C'est un peu hard pour un élève de terminale, mais j'ai l'impression que tu comprendras quand même.

Bonnes fêtes de fin d'année, et à bientôt.

BB.

A vous aussi