Inscription / Connexion Nouveau Sujet
Vecteur vitesse et vecteur accélération
Bonjour!
J'aurais besoin d'un coup de main pour commencer un exercice qui me pose problème! Merci d'avance pour toutes aides apportées!
Voici mon énoncé:
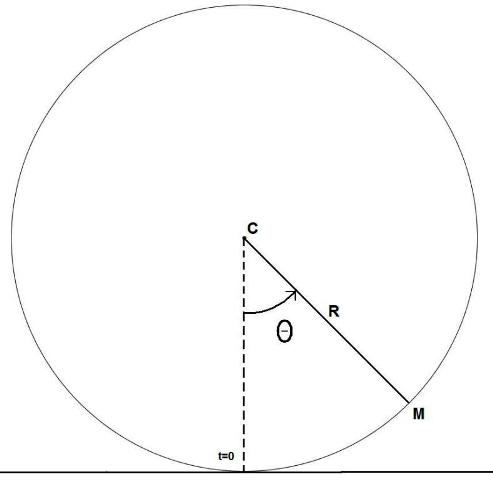
Une roue de rayon R et de centre C roule sans glisser sur un sol plat. Le mouvement de la roue est paramétré par l'angle  dont elle a tourné à partir de sa position initiale.
dont elle a tourné à partir de sa position initiale.
1) Quelle est la relation donnant la distance parcourue par le point C?
2) Quelles sont les coordonnées du point M de la périphérie de la roue qui touchait le sol à t=0?
3) Exprimer les vecteurs vitesse et accélération en fonction de R,  et des dérivées de
et des dérivées de  .
.
En fait mon professeur de physique sachant que je suis intéressé pour entrer en classe préparatoire aux grandes écoles m'a donné cet exercice en plus pour ce long WE. Mais je n'arrive pas à le commencer...
Merci de votre aide
Je joint aussi un schéma que j'ai fait pour essayer de démarrer l'exercice...
Salut,
1. La roue de rayon R avance d'une distance D en faisant un angle  .
.
Alors D = R.
Remarque : si la roue fait un tour complet, elle avance de D = 2Pi.R qui est le périmètre du cercle.
2. Lorsque M touchait le sol, on avait à t = 0,  = 0.
= 0.
3. Pour pouvoir déterminer la vitesse et l'accélération du point M, il faut passer par les coordonnées polaires.
On pose x = R.cos et y = R.sin
et y = R.sin
![]()
(tu supprimes la coordonnée z et ici r = R = constante).
Dans un premier temps, il vaut mieux calculer la vitesse de M par rapport au centre C du cerceau, c'est plus facile.


