Niveau terminale

vecteur accélération

Posté par
lisarib 19-01-19 à 22:22

Bonjour,

Tout d'abord, les flèches signifieront qu'il y a un vecteur.
Pour démontrer la formule de l'accéleration d'un mouvement ciruculaire ( a = (dv/dt)*T + ( v^2/r)*N)
, mon professeur est passé de (dT/dt) * v à ( v^2/r)*N. Pouvez-vous m'expliquer cette transition?

Posté par re : vecteur accélération 20-01-19 à 00:14

personne pour me répondre?

Posté par re : vecteur accélération 20-01-19 à 00:16

Il y a un autre soucis, à la suite du cours, pour les mouvements circulaires uniformes, il est dit que a = (dv/dt)*T + ( v^2/r)*N^2 .
Pourquoi le N devient N^2 ?

Posté par re : vecteur accélération 20-01-19 à 01:00

Bonsoir,
explication de la transition :

Vecteur vitesse dans le repère de Frenet : $\overrightarrow{V}=V \overrightarrow{T}$ . Le vecteur vitesse est porté par la tangente à la trajectoire.

Le vecteur accélération s'obtient en dérivant le vecteur vitesse :
$\overrightarrow{a}= \dfrac{dV}{dt} \overrightarrow{T}+V \dfrac{ \overrightarrow{dT} }{dt}$ (Relation 1 )

Exprimons les vecteurs mobiles $\vec T$ et $\vec V$ dans la base fixe $O, \vec i, \vec j$ :

$\vec{T}=-sin(\theta)~\vec{i}+cos(\theta)~\vec{j}$
$\vec{N}=-cos(\theta)~\vec{i}-sin(\theta)~\vec{j}$

Calculons $\dfrac{ \overrightarrow{dT} }{dt}$ :

$\dfrac{d \vec T}{dt}=-cos(\theta). \dfrac{d \theta}{dt}~\vec{i} - sin(\theta). \dfrac{d \theta}{dt}~\vec{j} =\dfrac{d \theta}{dt}~\vec{N} \\ \\ \dfrac{d \theta}{dt}= \dfrac{V}{R} \\ \\ \dfrac{d \vec T}{dt} = \dfrac{V}{R}~\vec N$

Retour à la relation 1:

$\overrightarrow{a}= \dfrac{dV}{dt} \overrightarrow{T}+ \dfrac{V^2}{R}~\vec N$

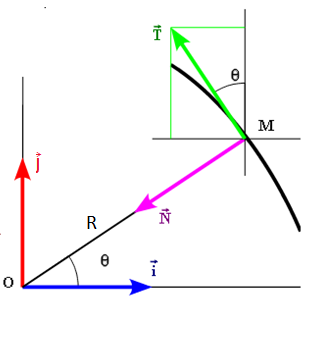
vecteur accélération

Posté par re : vecteur accélération 20-01-19 à 01:02

Je n'ai pas d'explication pour "l'autre souci ".

Posté par re : vecteur accélération 20-01-19 à 11:19

Comment trouve-t-on que vecteur T = -sin(theta) * vecteur i + cos(theta) * vecteur j , et de même avec le vecteur N?
De plus je pense ne pas comprendre les dérivées de vecteurs car je ne vois pas comment vous trouvez que la dérivée du vecteur T = -cos(theta)* dérivée ...
Merci de m'éclairer svp.

Posté par re : vecteur accélération 20-01-19 à 12:18

1) Comment trouve-t-on que vecteur T = -sin(theta) * vecteur i + cos(theta) * vecteur j , et de même avec le vecteur N?

Tout simplement en projetant les vecteurs $\vec T$ et $\vec N$ sur la base $O,\vec i,\vec j$

------------------------------------------------------------------

2) je pense ne pas comprendre les dérivées de vecteurs car je ne vois pas comment vous trouvez que la dérivée du vecteur T = -cos(theta)* dérivée ...

Je ne peux pas faire dans le cadre de ce forum un cours de mathématiques sur la dérivée des vecteurs.
On a ici :

$\vec{T}=-sin(\theta)~\vec{i}+cos(\theta)~\vec{j}$

Le vecteur $\vec{T}$ n'est pas un vecteur fixe, sa direction change en permanence.
La dérivée par rapport au temps de ce vecteur ( voir un cours de maths sur cette question ) est :

$\dfrac{d\vec T}{dt}= \dfrac{d\vec T}{d\theta}\times \dfrac{d\theta}{dt} =-cos(\theta). \dfrac{d \theta}{dt}~\vec{i} - sin(\theta). \dfrac{d \theta}{dt}~\vec{j}$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

vecteur accélération

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique