Inscription / Connexion Nouveau Sujet
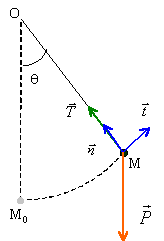
vecteur acceleration
Bonsoir j aurai une petite question, pour un pendule dont le mouvement est circulaire et non uniforme, est il possible que ce vecteur soit égale à zéro à un moment donné ?
Je vous remercie
Salut,
Si tu imagines un pendule, tu tiens la masse puis tu la lâches.
Celle-ci prend de l'accélération, puis ralentit, avant de faire le parcours inverse et ainsi de suite.
Donc ?

Bah non elle est maximale à ce point.
C'est au point M, là où la vitesse devient nulle, avant que le pendule reparte dans l'autre sens 
Ah oui merci
Donc pour calculer une accélération on ne se sert pas de la valeurs des vecteurs vitesse mais bien du delta lu sur le graphique auquel on aurait appliqué une échelle