Hello

Peux tu préciser où est ce que "ça coince"?

Tous ces exercices commencent de la même façon:

1) on fait un beau dessin
2) on se donne un référentiel (galiléen si possible)
3) on prend bien note des conditions initiales
4) on fait le bilan des forces
5) on écrit la relation fondamentale de la Dynamique (avec les Théorèmes de l'energie cinétique et de la mécanique sous la main pour le cas ou)
6) ensuite c'est variable, mais généralement on projète sur les axes du référentiel

A toi?

Bonsoir, en faites la physique et moi ça fait 2, et je ne comprend juste pas le procédé qu'il faut utiliser pour chaque question, s'il faut répondre avec des formules, ou dessin..

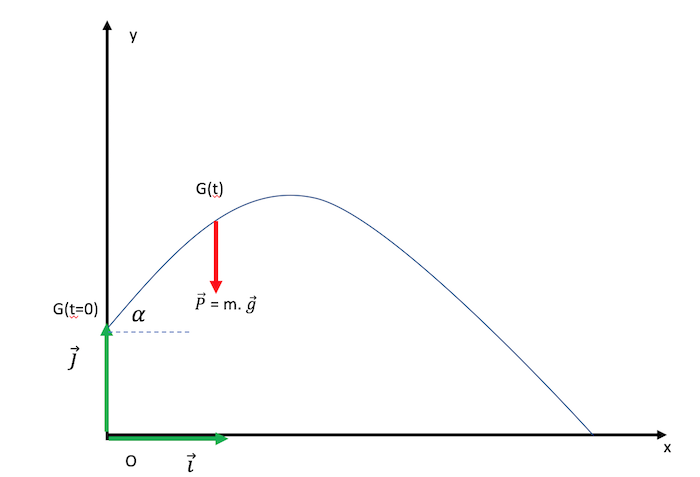
On étudie la mouvement de la balle dans le référentiel terrestre (galiléen pour cette expérience) muni d'un repére orthonormé (0,) tel que représenté

On néglige les forces de frottements (car l'énoncé n'en fait pas mention ... )

Dans le référentiel G est soumis à son seul poids.

La relation fondamentale de la dynamique nous dit alors:



Peux tu projeter cette égalité vectorielle sur les axes Ox et Oy ?

Désolé mais je ne comprend vraiment pas..

Faisant l'hypothèse que tu as appris un minimum de cours, c'est à dire que tu sais:

- ce qu'est un référentiel, ce qu'est un référentiel galiléen

- ce qu'est la relation fondamentale de la dynamique

- projeter des vecteurs sur les axes d'un repère

Je souhaiterais que tu précises ce que tu ne comprends pas. Il est très difficile de répondre à une phrase générale "je ne comprends autrement que par des généralités.

Je suis en prépa à distance, et je n'ai pas de professeurs pour m'expliquer. J'ai juste un cahier de cours, mais ce que je ne comprend pas ce sont les explications de mon cours, ce qui m'empêche donc de faire mes exercices correctement. Merci quand même de votre aide, je vais me débrouiller.

hop hop hop, on ne va pas se décourager si vite.

1) Référentiel galiléen: OK pour toi? Si ok, tu comprends que dans ce référentiel pour pouvoir mesurer position, vitesse, ... j'ai besoin d'un repère dans l'espace c'est à dire d'une origine (le point O qui aura des coordonnées de position nulles) et 3 axes pour mesurer des coordonnées.  Un système de mesure fondamental consiste à prendre des axes type "règle graduée" qui retournent 3 coordonnées cartésiennes x, y et z

C'est l'objet du dessin d'hier . Je définis une origine: le point O et 2 axes (parce que le mot se fera dans un plan, donc un 3eme axe ne me sert à rien).  x horizontal et y vertical

2) Ensuite comme le référentiel est galiléen, je peux y appliquer, pour mon système (la balle) la relation fondamentale de la dynamique (2nde loi de Newton)

Qui dit que    

Où les forces prises en compte sont les forces extérieures que subit le système (la balle toujours)
m est la masse du système
et son accélération

Est ce qu'arrivés là, nous sommes "nominaux"? Ou bien est ce que ça frotte déjà qlq part? Et ou?

Merci  dirac!

J'ai bien compris jusqu'ici, mais  pour moi il n'y a pas de frottements car le seul force exercée sur cette balle est son poids ?

Bon, le décor est planté, on a un repère ...

Quand j'écrivais "est ce que ça frotte déjà qlq part", je faisais allusion à ta bonne compréhension de ce que j'écrivais ...   ça m'apprendra à utiliser des métaphores ...

Oups je n'avais pas compris la blague

\vec{P} = m.\vec{a}
donc m\vec{a}  = mg soit \vec{a} =g

J'ai essayer de faire les questions 1a, b, c et d, mais je ne sais pas si cela est correct...
Pour la réponse 1a, j'ai utilisé les trois axes, x,y,z.. j'ai répondu :
{ax=0
{ay=0
{az=-g

1b)

{Vgx=0
{Vgy= Vo*cos
{Vgz= -gt+Vo*sin

1c)

équations horaires:
{x(t)=0
{y(t)= Vo*cos*t
{z(t)=-1/2*g*t²+Vo*sin*t

1d)

t= (y/Vo*cos)
Ce qui donne : y= -1/2*g*(y/Vo*cos)²+Vo*sin*(y/Vo*cos)

y= -1/2*(y/Vo*cos)² + tan y.

2a) La direction du vecteur Vs est verticale et le sens est vers le bas.

J'aimerais savoir si mes résultats sont correctes où si j'ai fais des erreurs
Je bloque pour la suite, je ne vois pas comment déterminer à quel instant la balle atteindra le sommet, ni la vitesse

2b) j'ai utilisée la formule suivante : Ts= Vo/g soit 20/10=2

2c) La balle ayant atteint son sommet, sa vitesse sera nulle.

Est-ce correct ?

Tu auras noté que "mon" repère est dans un plan vertical (car la trajectoire de la balle se fait dans un plan vertical) -> on a besoin que de 2 coordonnées

J'ai appelé x l'axe horizontal
Et y l'axe vertical

Tu as finalement décidé d'appeler z ce qui est y sur le schéma et d'appeler y ce qui est x . Soit, on va suivre tes notations  ... la prochaine fois je ne me fatiguerai pas à faire un beau dessin

Donc, après double intégration et prise ne compte des conditions initiales, on arrive à



Eh oui! il est dit dans l'énoncé que la balle est lancée depuis une hauteur h = 1 m  donc z(t=0) = h  (ce que j'avais matérialisé d'ailleurs sur mon très beau dessin :P )

Ensuite, à l'erreur ci dessus près, tu à bien compris qu'il fallait éliminer le paramètre t pour trouver une équation z = z(y)

Je te laisse reprendre ce passage...

Pour poursuivre,

Le sommet est le maximum de la coordonnée z(t)

Donc en S   dz/dt = vz = 0  (la composante verticale de la vitesse est nulle!  Pour faire simple: la balle a fini de monter -en montée vz > 0 - et n'a pas encore commencé à descendre -en descente vz < 0- donc vz = 0)

Pour résumé, en S:     vy = v0cos   et vz = 0

(vs est horizontale,  orientée dans le sens positif de l'axe Oy    )
  
Or  

Avec vz(t=ts) = 0

Donc

Je te laisse reprendre la main? Enfin le clavier ...

Il est important que tu sois au point sur les réponses apportées jusque là avant d'attaquer l'ascension finale de la question 3)

J'ai donc continuer avec 2 axes comme tu me l'as conseillé!

Je vais corriger mes erreurs, je crois que j'ai enfin compris, merci

Juste pour la question 2b, est ce que je peux justifier par une phrase en expliquant que comme elle a atteint son maximum sa vitesse est nulle, ou faut-il que je justifie avec les formules ?

La question 2b) était "à quel instant ts la balle atteint elle de sommet S"

Je répondrais de la manière suivante:

S est le sommet de la trajectoire, donc  vz(t=ts) = 0

Or vz(t) = -gt+v0sin,

Donc  -gts + v0sin = 0, soit   ts = v0sin/g

Merci pour votre avis