Inscription / Connexion Nouveau Sujet
Variation de l'énergie mécanique (2)
Re-bonjour, voici le même genre d'exercice que mon 1er post :
C'est un skieur de masse 80 kg tracté par une perche d'un téléski sur une partie BC montante rectiligne : BC = 50m.
En B la piste est inclinée d'un angle 
et elle exerce sur l'ensemble (skieur + ski) une force de frottement f de valeur constante 40 N et parallèle à la piste. La tension exercée par la perche reste inclinée de l'angle 
par rapport à la piste et est maintenue à une valeur telle que la vitesse reste égale à la valeur acquise en B (soit 10,8 km/h)
Données : BC = 50 m; sin = 0,25; cos= 0,96; sin = 0,8
1. Après avoir fait le bilan des forces appliquées au skieur exprimer la variation de l'énergie mécanique entre B et C et déterminer la tension T de la perche supposée constante.
2. Retrouver ce résultat en appliquant une loi de newton au skieur.
1. Em= Ec + Epp or Ec = 0 parce que la vitesse reste constante.
Donc Epp = mgz avec z : cos=BK/BC <=> 0,96 = BK/50 <=> BK = 0,96*50= 48m (K est le nom que j'ai donné pour faire un triangle rectangle)
D'après le théorème de Pythagore : BC²=BK²+KC² <=> 2500 = 2304 + KC² <=> 196=KC² <=> 
196 = 14m
Soit Epp = 80*10*14= 11200 J
Donc 
Em=Epp=
Fextérieur = F*BC*cos-f
<=> F = (11200)/50*cos-f = (11200)/48-40 = 1400 N
2. J'applique la 1ère loi de Newton et on trouve 240 N (et je pense que c'est le bon résultat)
Donc pourquoi je trouve une valeur si élevé à la question 1 (pour une fois que j'avais un raisonnement... ^^) Que fallait-il faire ?
Merci beaucoup en espérant qu'il ne manque pas d'info pour comprendre !
Boal
Re - bonjour,
Alors, on continue !
Allons-y doucement :
Bilan des forces appliquées
Pour chaque force, s'il te plaît,
. point d'application (le skieur, considéré comme ponctuel)
. direction
. sens
. intensité (calculée ou littérale) avec son unité
Bilan des forces :
Rn = surface du ski/sol, vertical vers le haut et intensité : Rn= P sin
f = surface du ski/sol, horizontalement incliné, orienté dans le sens contraire de la projection sur x, intensité
f=40 N
T = skieur, horizontalement incliné de cos par rapport à la piste et orientée dans le sens de la projection x, intensité T = 240 N (normalement)
P = skieur, vertical vers le bas et intensité P = mg = 800 N
Rien ne vaut un schéma :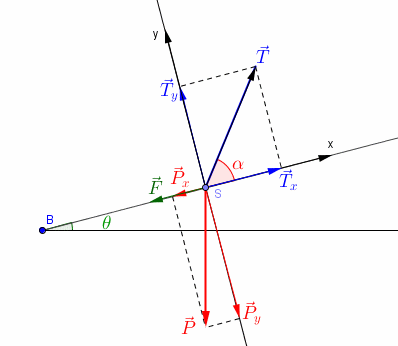
Je l'ai fait rapidement sans rechercher aucunement à respecter des échelles de force.
BS : le plan incliné d'un angle par rapport à l'horizontale
S : le skieur
Sx : l'axe de projection, selon le plan incliné et orienté dans le sens de la montée
Sy : le deuxième axe de projection, perpendiculaire au plan incliné, orienté vers le haut : le poids, direction verticale, sens vers le bas, intensité 800 N
: la traction de la perche, direction faisant un angle
avec le plan incliné, sens vers le haut, intensité à rechercher : les forces de frottement, direction selon le plan incliné, sens opposé au mouvement donc vers la descente, intensité 40 N
Le schéma faut aussi apparaître les vecteurs, composantes du poids et composantes de la force de traction selon les axes Sx et Sy
___________
Quelles sont les forces qui travaillent ? Travail moteur ? Travail résistant ? Que peux-tu dire en termes d'énergie ?
La force motrice : Traction de la perche
Terme d'énergie ? : Positive
Les forces résistantes : Poids et frottement.
Termes d'énergie : frottement négatif
Force motrice : la traction exercée par la perche
Forces résistantes : le poids et les frottements
En termes d'énergie :
L'énergie potentielle de pesanteur du système Terre-skieur est augmentée (travail résistant du poids).
Il y a une autre énergie qui apparaît ? Laquelle ? Elle est due au travail de quelle force ?
ah ok...
- Epp (donc Energie mécanique)
- Travail de la traction exercée par la perche. (W(T) = T*AB = T*AB*cos
Oui, l'énergie mécanique. Ici l'énergie cinétique ne varie pas puisque la vitesse est constante. L'énergie potentielle de pesanteur du système Terre-skieur augmente puisque le skieur se trouve à la fin à une hauteur plus élevée qu'au début.
Mais une autre force travaille qui transfère de l'énergie (prélevée à l'énergie mécanique délivrée par la seule force motrice : la traction de la perche) ; quelle énergie apparaît suite au travail des forces de frottement ?
Oui, énergie thermique.
Il est sûr que si l'on fait un bilan d'énergie (de travail des forces) il ne va pas falloir oublier cette énergie qui n'est pas de l'énergie mécanique (au sens macroscopique). L'énergie mécanique (cinétique + potentielle de pesanteur) se conserve seulement pour un système isolé, donc sans frottements...
___________
Alors on peut maintenant calculer tous les travaux de toutes les forces qui travaillent.
(Ne me redonne pas les valeurs de ton premier message ; malheureusement les deux questions y sont fausses ; conseil : ces exercices que nous faisons ensemble, mets-les de côté quelques jours - un peu pour les oublier - et refais-les tout seul pour vérifier que tu as compris et sais les refaire ; cela te sera profitable).
Mon Epp = 11 200 J est fausse ? Pourtant je pensais (^^) avoir calculé la hauteur "vertical" (=altitude) de la piste que le skieur était en train de monter (qui était un dénivelé de 14m ...)
W(T) = vec T * vec BC = T*BC*cos () ? (vec = vecteur)
W(f) = vec f * vec BC = f*BC*cos 0 (=1) ? (par rapport à la piste le cos)
W (Et (=energie thermique)) = vec Et + vec BC = Et*BC*Cos 0 (=1)
c'est vrai que je suis très étonné qu'on doit faire intervenir l'énergie thermique dans ce genre d'exercice, donc je ne sais pas trop comment m'y prendre...
Em = 
Fext = W(T)+ W(f) + W(Et)
ça ne risque pas d'être ça mais bon...
Tout d'abord je complète mon schéma : j'avais oublié une force : la réaction normale du support
: réaction normale du support, direction perpendiculaire au plan incliné, sens vers le haut, intensité inconnue
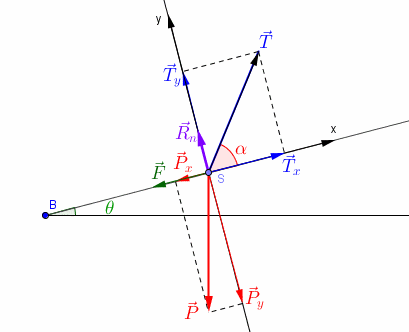
Cette force ne travaille pas puisqu'elle est perpendiculaire au déplacement.
________
Les trois forces (ou composantes de force) qui travaillent :
1) la traction qui est inclinée de
par rapport au déplacement, donc
WT = T.BC.cos()
Autre méthode : la composante Tx travaille et elle n'est pas inclinée par rapport au déplacement
WTx = Tx.BC
et comme Tx = T.cos()
on retrouve le même résultat (mais le raisonnement a été légèrement différent)
WTx = T.cos().BC
2) Le poids
Deux méthodes pour la même raison
Ou bien
WP = P.BC.cos[(
/2) + ] = - P.BC.sin()
Ou bien on considère la composante Px
WPx = - Px.BC (attention travail résistant, compté négativement)
comme Px = P.sin()
on retrouve une fois de plus le même résultat par cette autre méthode
3) les frottements
Travail résistant :
WF = - F.BC
Voilà pourquoi il est si important de bien faire le bilan des forces et d'y repérer celles qui travaillent, celles qui ne travaillent pas. Et, parmi celles qui travaillent, celles dont le travail est moteur et celles dont le travail est résistant.
_________
Je te laisse digérer cela. Pour ma part, j'arrête toujours à 22 heures (car j'ai commencé à 7 h 30...)
Bonne soirée et à demain pour la suite !
Je ne suis pas sûr de pouvoir beaucoup t'aider ce matin. Aussi je te donne quelques indications et le résultat numérique. À toi de dérouler toutes les démonstrations.
_________
Pour terminer la première question :
. calcul et somme des travaux résistants
. calcul (en partie littéral) du travail moteur
Si aucun travail n'a été oublié (et c'est pour cela que le bilan précédent était important) la somme algébrique des travaux moteur et résistants est nulle.
Ce qui permet une première valeur de
_ _ _ _
Deuxième question : oui, il faut bien appliquer la première loi de Newton (puisque le mouvement est rectiligne à vitesse uniforme)
Simple question de projections
_ _ _ _
Pour les deux questions, il n'est peut-être pas inutile de se rafraîchir la mémoire du côté des formules élémentaires de trigonométrie.
Pour les deux questions je trouve
_______
Mais bien sûr, en fonction de ma disponibilité, je répondrai à tes questions ou difficultés.
C'est bon j'ai tout trouvé, ce matin j'avais essayé, mais après une erreur de calcul mental (c'est un exercice sans calculette) toute bête je n'avais pas réussi. Mais cette après-midi c'est bon !
Merci d'avoir pensé à moi ce matin à 7h43 ^^ et merci de cette patience ...
Boal !
J'aurais aimé lire les démonstrations aux deux questions. Car il y a beaucoup à apprendre avec cet exercice qui est bien conçu.
Sinon, je t'en prie, bon courage et à une prochaine fois !
Alors :
BdF : W(T)= T.BC.cos() => W moteur
W(P)= - P.BC.sin() et W(f) = - f.BC => W résistants
Frésist : W(P) + W(F) = - P*BC*sin- f*BC = -800*50*0,25-40*50 = -12000 N
F motrice : W(T) = T*BC*cos = T*50*cos
Or cos = cos²+sin² = 1
soit 0,64 + cos² =1 <=> cos = 0,6
Donc : F motrice : W(T) = T*50*0,6 = T*30
Alors : -12 000 + T*30 = 0 <=> T = 12000/30 = 400 N
Syst = skieur => RTSG
D'ap la 1ère LN : P+Rn+f+T = 0 (en vecteur)
projection/x : -mgsin-f+T*cos <=> T = (mg*sin+f)/cos = 400 N
Voilà ! J'ai écris assez vite
Très bien !
Tu as vu ce qu'il fallait voir.
Je ne sais pas ce que tu penses de cette manière de t'aider.
Pour ma part, j'ai souvent apprécié les ouvrages qui, à la fin d'un exercice, en donnaient les résultats (sans donner la démonstration, le corrigé).
Cela permet de voir assez vite que l'on parvient (probablement avec une méthode correcte) à la solution. Et, dans le cas contraire, de voir qu'il faut chercher, passer du temps, reprendre le cours... parce que quelque chose ne va pas quelque part. Ton avis m'intéresse (au moins pour t'aider, car ce peut être une question de préférence personnelle).
C'est vrai que j'ai apprécié cette "méthode" pour m'aider et je suis plutôt partant pour continuer la dessus si possible. Parce que mon problème c'est que j'affronte pour la 1ère fois les exercices que je fais et je bloque très souvent parce qu'il me manque le raisonnement/la méthode, mais lorsque qu'on me dit dans quel sens aller ça va souvent mieux et après c'est à moi d'assimiler la méthode !
Annuler
connectez vous