Inscription / Connexion Nouveau Sujet
Une bille dans une glissière incurvée (dynamique)
Bonjour, j'ai un problème du quasi même type qu'hier:
Un solide ponctuel de masse m est lance avec une vitesse V0 sur une glissière circulaire de rayon r et de centre O. Les frottements sont négligeables. La position du mobile est repérée par l'angle THÊTA.
....... .
.
/ .
/ .
/ .
|THÊTA .
| .
________|__.
J'espere que vous comprendrez mon graphique fais avec amour mais surtout avec les moyens du bord 
Alors voilà je dois exprimer la réaction Rn de la glissière sur la bille
Bon alors je m'y prend comme ceci:
2nd lois de Newton :
P+Rn=m*an (Rn ayant le même sens que an car la bille étant DANS la glissiere)
Pour l'instant c'est bien juste?
Ensuite petit problème concernant notre angle THÊTA... Il ne s'inscrit pas dans un triangle rectangle donc impossible d'y exercer la loi sin cos tan.
Je pense qu'il serai judicieus de travailler avec l'angle THÊTA' tel que
THÊTA'=180-THÊTA ?
Mais au final avec sa je trouve :
Rn:mg(-3cosTHETA'+2)
Mais ma correction me donne un autre résultat:
Rn=m(V0² /r)+mg(3cosTHETA-2)
Pouvez vous me montrer le bon calcul correspondant?
Bonjour,
C'est exactement le même raisonnement que pour la bille glissant sur la sphère.
Il faut juste tenir compte du fait que la bille a une énergie cinétique initiale
donc la conservation de l'énergie mécanique donne:
1/2 mv2 + mgh = 1/2 mv02
avec h = R - Rcos
pour le schéma il faut prendre  < 90° de préférence
< 90° de préférence
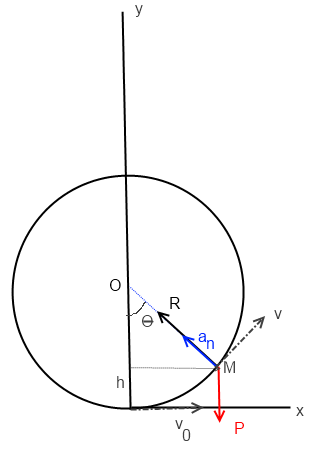
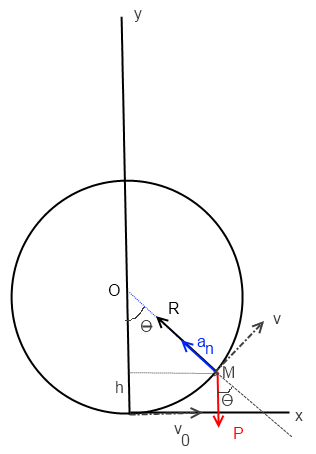
tu prends les angles que tu veux du moment que tu projettes correctement les forces avec tes angles
c'est plus facile avec des angles < 90°
je ne vois pas l'intérêt d'une figure avec  > 90° ici
> 90° ici
d'autant que le résultat obtenu avec ma figure vaut aussi pour  > 90°
> 90°
Ok j'ai donc effectué mon calcul avec un angle THÊTA <90
Mais je ne trouve toujours pas le bon résultat.
Rn est orienté cette fois ci vers l'intérieur du virage donc de même signe que an:
-P+Rn=m*an
Rn=m*an+P
--------> au final je trouve:
Rn=m(V0² /r)+mg(cosTHETA+2)
Ce résultat me semble juste mais la correction en affirme une autre et je comprend pas car on dirait qu'ils ont orientés Rn vers L'EXTÉRIEUR :
Rn=m(V0² /r)+mg(3cosTHETA-2)
Rn est donc dirigé vers l'intérieur ou l'extérieur et quel est le bon résultat selon vous?
Merci bonne matinée
h = R(1 - cos(theta))
(1/2).m.v² = (1/2).m.Vo² - mgR(1 - cos(theta))
v² = Vo² - 2gR(1 - cos(theta))
Fc = m.v²/R
Fc = m.[Vo² - 2gR(1 - cos(theta))]/R
Fc = m.[Vo²/R - 2g(1 - cos(theta))]
Composante normale du poids = mg.cos(theta)
---
réaction du support :
N = m.[Vo²/R - 2g(1 - cos(theta))] + mg.cos(theta)
N = m.[Vo²/R - 2g(1 - cos(theta)) + g.cos(theta)]
N = m.[Vo²/R - g(2 - 3cos(theta))]
-----

À oui je ne dois pas oublier De changer de signe lorsque le travail est dit résistant.
Merci et à bientôt
la composant normale du poids ne travaille pas, de même que la réaction, puisque ces forces sont perpendiculaires à la trajectoire!
je pense que tu est "fâché" un peu avec la projection des forces sur un axe
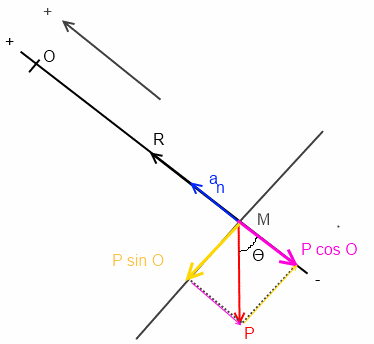
Lorsqu'on projette les forces sur la normale en orientant OM dans le sens positif de M vers O alors on trouve:
man = R - P cos
(voir le schéma ci -dessous)
le signe moins devant P cos O provient uniquement de l'orientation de la normale OM que tu as choisie, pas d'autre chose.
supposons que tu orientes OM dans le sens positif de O vers M
alors tu écriras:
-m an = - R + PCos O (ce qui est équivalent, l'orientation ne change pas le résultat, c'est une convention, mais il faut s'y tenir! )