Bonjour.

Si O désigne le centre de l'écran d'observation, et B_k le centre de la k^ième frange brillante, on peut écrire OB_k = k i   (avec k entier).

Comme vous avez ici deux radiations, vous pouvez écrire deux relations :
OB_k1 = k₁ i₁     et     OB_k2 = k₂ i₂

Déterminez ainsi les positions des franges brillantes des deux systèmes d'interférences et vous trouverez les coïncidences.

Au revoir.

Bonjour à tous les deux,

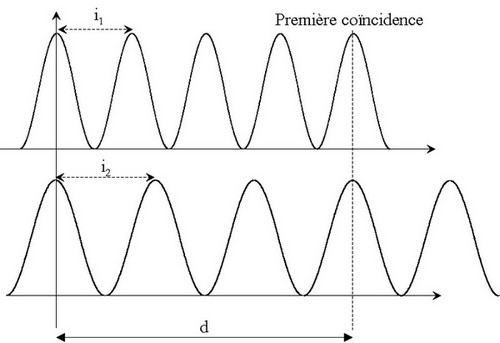
j'ai passé un peu de temps à faire le schéma ci-dessous ...

Benjabesoindaide, ton petit problème n'en est pas un :

Soit d cette distance à trouver, i₁ l'interfrange dû à la longueur d'onde la plus petite (467 nm), et i₂ celui correspondant à la plus grande (700 nm).
Le schéma montre que la coïncidence arrivera quand d sera égale à n fois i₁ et (n-1) fois i₂, OK ? Sur mon schéma n vaut 4, mais tu obtiendras une valeur sûrement plus grande.
Alors on écrit n.i₁ = (n-1).i₂ soit (n-1)/n = i₁/i₂, dont on tire facilement n connaissant le rapport des interfranges.
Ce rapport est d'ailleurs connu, car il est égal au rapport des longueurs d'onde, 467/700.

Une fois n connu, il suffit de calculer i₁ pour obtenir d = ni₁, ou i₂ pour obtenir d = (n-1)i₂.

erratum... sur mon schéma n = 4, il faut regarde la première figure d'interférence.

Bonjour Prbebo.

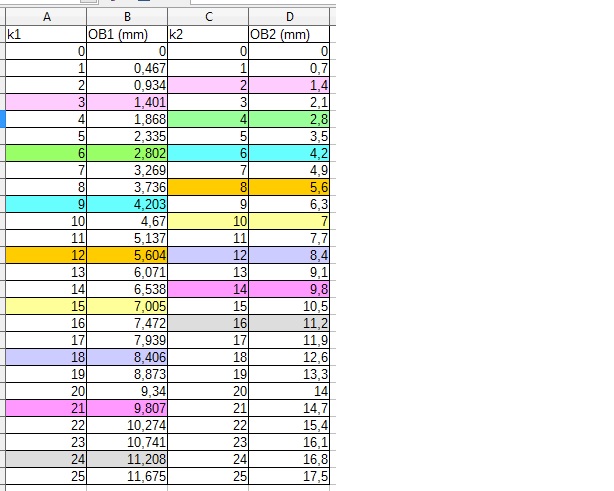
En utilisant un tableur, j'obtiens la première coïncidence à la distance OB₁ = 3 i₁ = 3 * 0467 = 1,401 mm soit k₁ = 3
et OB₂ = 2 i₂ = 2 * 0.700 = 1,400 mm soit k₂ = 2

Bizarre ce décalage d'entier.

Bonjour Picard,

non ce n'est pas bizarre, la bonne réponse est en effet 2 interfranges pour i₂ (700 nm) et 3 interfranges pour i₁ (467 nm). C'est ce que j'obtiens en faisant l'application numérique de ma relation (n-1)/n = i₁/i₂ qui, arrangée un peu, donne n = i₂ / (i₂-i₁). Ce qui donne n = 3 et confirme les résultats de ton tableur.

En revanche, je reconnais bien volontiers que ton raisonnement est plus rigoureux que le mien, car je me suis placé sans réfléchir dans un cas particulier, celui où les nombres d'interfranges à la superposition des franges brillantes diffère d'une unité (pour Benjabesoindaide : n pour l'une, n-1 pour l'autre). Et, coup de chance pour moi, c'est le cas dans cet exercice ! D'ailleurs j'ai oublié dans mon post précédent de préciser une condition importante : le nombre n calculé ainsi doit être un nombre entier ; une valeur décimale aurait signalé qu'à la coïncidence les nombres d'interfranges pour chaque longueur d'onde diffèrent de deux ou plus.

Alors, pour Benjabesoindaide, permets-moi de retenter ma chance en reprenant ton raisonnement :

A la superposition de deux franges brillantes on a en effet : k₁.i₁ = k₂.i₂, où k₁ et k₂ sont deux nombres entiers quelconques, sans rapport entre eux. Ceci donne k₁/k₂ = i₂/i₁ = ₂/₁.

On en déduit que le rapport des longueurs d'onde doit se présenter comme une fraction rationnelle. Comme ces deux longueurs d'onde sont des nombres entiers, une solution évidente est k₁ = 700 et k₂ = 467, mais ce n'est pas forcément la bonne car il peut y avoir des coïncidences bien avant de compter autant de franges. Pour le savoir, il faut mettre la fraction 700/467 sour forme irréductible, donc rechercher le PGCD de ces deux nombres. L'algorithme d'Euclide (souvenir de troisième...)  donne facilement le PGCD de 700 et de 467 : c'est à peu de choses près 233, car 233x3 = 699 700, et 233x2 =466 467.

Donc 700/467 = 3/2, cette fraction étant maintenant irréductible, on obtient bien k₁ = 3 et k₂ = 2... sans tableur .

Mon raisonnement est valable lorsque les deux longueurs d'onde sont très proches l'une de l'autre (les deux composantes du doublet jaune du sodium par exemple, avec 589,00 nm et 589,59 nm). Dans cette situation il faut aller rechercher la coïncidence très loin, n est donc très grand (999 pour le sodium) et il n'y aucun risque à l'arrondir à l'entier le plus proche.

Benjabesoindaide, j'espère que tu as compris tous les aspects de cette question.

Picard, merci de m'avoir repris sur mon post d'hier ! Mais une erreur n'est jamais grave tant qu'elle débouche sur quelque chose de constructif.

Bon dimanche à tous les deux.

B.B.

Pas de problème Prbebo !

Juste pour le fun...

OB_k1 = k₁ i₁ et OB_k2 = k₂ i₂     avec k₁ et k₂ entiers et i₁ < i₂

On peut donc écrire :     k₁ = k₂ + n    avec n lui aussi entier.

Soit : (k₂ + n) i₁ = k₂ i₂
On tire : n i₁ = k₂ (i₂ - i₁)


C'est à dire : k₂ =


numériquement : k₂ = = 2 n

La première coïncidence (hors n = 0 qui correspond à la frange centrale) est obtenue pour n = 1    soit   k₂ = 2   et   k₁ = k₂ + n = 2 + 1 = 3

On s'amuse, on s'amuse !!!

Ma fois, je n'avais jamais pensé à ça ! On apprend à tout âge, y compris au mien...
A bientôt sur le forum.

PS, je te laisse continuer avec Marguerite (les anneaux de Newton avec un miroir et une lame à faces parallèles), ça m'a l'air de ramer sec de son côté...

BB.