Inscription / Connexion Nouveau Sujet
Un exercice de physique avec force
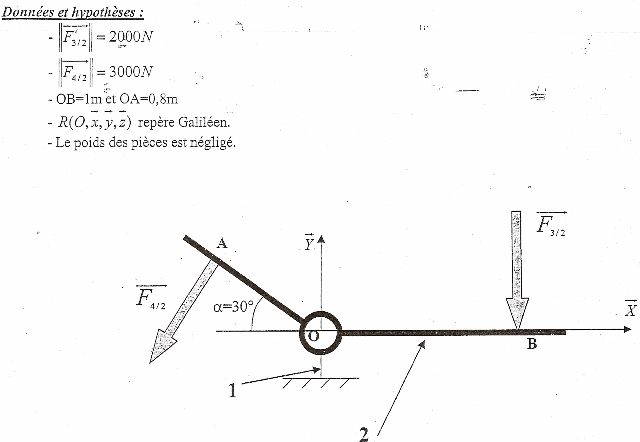
Question 1 : calculer les composantes de F3/2 et F4/2
Question 2 : calculer au point O Mo(F3/2)
Question 3 : Calculer au point O le moment Mo(F4/2) par deux méthodes différentes
Question 4 : Calculer au point O, le moment résultant de deux moments précédemment calculés
Question 5 : conclure
Question 6 : Déterminer la norme de F3/2 pour que le moment résultant au point O soit nul
ps: je n'arrive pas a joindre le shema..
Tous d'abord merci de m'aider ,
J'aurais besoin d'aide car je ne sais dutout comment m'y prendre, par quoi commencer...
Pour calculer les composantes d'une force, il faut les "projeter' sur X et Y. avec les sinus et cosinus c'est un jeu d'enfant! =)
Je te le fais pour F3/2
Projection sur x: 0
Projection sur y: -200
car F3/2 parallèle à y mais de sens opposé
C'est 2000 plutot mais je penses qui faut projeter sur y aussi...
Et pour F4/2 je met cos 30 , sin 60 * -3000 ?
19h21 répondait à ton message de 19h12
pour répondre à 19h20
les données indiquaient 2000 (j'aurai donc dû écrire -2000)
F3/2 est perpendiculaire à x => F3/2 sur x =0
F3/2 parallèle ç y mais y vers le haut et F3/2 vers le bas donc F3/2 sur y = -2000
Et pour F4/2
projection sur x : cos 30
projection sur y : (sin 60 * -3000)
Projection sur z : 0
Est ce bon ?
non
dans cosinus et sinus il faut le même angle ( la valeur de alpha) de plus sur x il manque le 3000 et la projections sur x n'a pas le bon signe.
donc projection sur x : -sin 30 *3000
projection sur y : -cos 30 * 3000
tu peux m'expliquer comment tu raisonnes, je vois pas dutout la ...
Le moment d'une force en un point est la norme de la force multiplié par la distance entre me point d'application de la force et le point. donc ici Mo(F3/2) = ob.F(3/2)
Il faut bien comprendre ce qu'est un moment, une fois que c'est compris, ça passe tout seul, j'avais un peu de mal aussi au début!
En moment, c'est en fait, un couple (c'est l'appellation la plus commune). Le moment, c'est ce qui provoque une rotation ;
Exemple méga concret : quand tu ouvres une porte, ta main exerce une force sur la poignée, donc tu vas exercer un moment sur le pivot de la porte, qui va la faire ouvrir. Ce moment s'écrira :
Mo(Fmain/porte) : (Dist Poignée/porte) x (force exercée sur la poignée).
J'espère que j'ai été clair, cette notion de moment est hyper importante en SI, mais une fois qu'on comprend ce que ça représente physiquement, c'est gagné. 
On prend la même méthode que le 2, c'est la même chose! Il ne faut pas oublier les propriétés du vecteur. on a affaire ici à un vecteur représentant un traction, avant, il représentait une poussée (grossièrement). C'est donc la même chose que le 2...
2eme méthode ; princpe fondamental de la statique!
Somme des forces et des mo..... = 0, tu vois de quoi je parles? 
Alors je fais Mo(F4/2) = Oa*F4/2
= 0.8* -3000
est ce cela ?
euh un peu .. mais je galeres avec sa...
c'est ça sauf que Mo(F3/2) et Mo(F4/2) ne font pas tourner le système dans le même sens donc ils sont de signe opposés.
ce calcul montre aussi que Mo(F3/2)+Mo(F4/2) 0
0
De signe opposé mais j'ai mes deux moments qui sont négatifs...
j'ai Mo(F4/2) = OA*F(4/2)
= 0.8* -3000
Et Mo(F3/2)= OB.F(3/2)
= 1* -2000
si il n'y avait que F3/2 dans quel sens tournerait le système?
si il n'y avait que F4/2 dans quel sens tournerait le système?
choisis un sens positif
c'est ta phrase qui n'a aucun sens
vecteur moment F3/2 = produit vectoriel(vecteur OB;vecteur F3/2)
donc vecteur F3/2 est sur l'axe z
si il n'y avait que F3/2 dans quel sens tournerait le système?
si il n'y avait que F4/2 dans quel sens tournerait le système?
choisis un sens positif (de préférence prends le sens trigonométrique comme sens positif)
Mo(F4/2) = OA*F(4/2) = signe(Mo(F4/2))*I0.8* -3000I
Mo(F3/2)= OB.F(3/2)= signe(Mo(F3/2))*I 1* -2000I
il faut plutôt dire le moment de la force est positif ou négatif
donc qu'obtiens tu comme moment pour F3/2 et F4/2
Mo(F4/2) = OA*F(4/2) = signe(Mo(F4/2))*I0.8* -3000I
= - 0.8* -3000 = 2400
Mo(F3/2)= OB.F(3/2)= signe(Mo(F3/2))*I 1* -2000I
= + 1 * -2000 = -2000