Inscription / Connexion Nouveau Sujet
Tremplin de saut à ski
Bonjour!
Je n'arrive pas à faire deux questions de cet exercice, je trouve des résultats non probable. 
Voici l'énoncé :
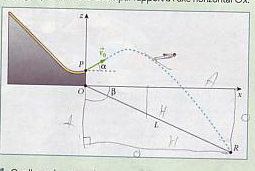
Un champion de saut à ski, assimilable à un corps ponctuel, s'élance sur un tremplin de saut à ski. Au moment d'aborder le saut, sa vitesse initiale Vo est égale à 25m.s^-1. Le bas de la piste est en outre incliné vers le haut d'un angle  égal à 10°.
égal à 10°.
Le skieur quitte la piste au point P.
On associe au référentiel terrestre le repère (0, vect(i), vect(k)). Le point P se situe à 6m à la verticale du point O. La piste de réception fait un angle  =50° vers le bas par rapport à l'axe horizontal Ox
=50° vers le bas par rapport à l'axe horizontal Ox
Dans la première et deuxième question on doit trouver l'équation cartésienne de sa trajectoire soit
Z= -0.5g * ( x / (Vo*cos ))² + x*tan
))² + x*tan  + Zp
+ Zp
Pas besoin de vérifier, nous avons trouvé cette formule en classe.
3) Quelle est l'équation de la droite représentant la piste de réception.
On sait qu'une équation de droite s'écrit sous la forme y=ax+b, dans notre cas, b=0 et a= cos  * L soit y=(cos
* L soit y=(cos  * L)x
* L)x
4)Le skieur se réceptionne au point R. Quelles sont les coordonnées de ce point ? Quelle est la longueur L du saut (L=OR) ?
Pour les coordonnées de R, j'ai mis :
R ( x=sin  *L ;z=cos(90-
*L ;z=cos(90- ) * L )
) * L )
J'ai essaye de resoudre l'équation en isolant x pour trouvé L mais j'ai trouvé L=1.31m 
Ensuite je l'ai refait en utilisant l"équation cartésienne de la trajectoire que j ai injecté dans l'équation z=cos(90- )*L mais cette fois ci, je trouve 5m
)*L mais cette fois ci, je trouve 5m 
Bonsoir,
Pour b, j'aurais plutôt dit que le coefficient directeur (ou pente) de la droite est égal à tan et que, de plus, la pente est négative donc z = -x tan
et que, de plus, la pente est négative donc z = -x tan .
.
Nous avons donc :
zR = -0,5g( xR/(Vo*cos))2 + xR tan + zP
+ zP
et, d'autre part, :
zR = xR tan
Donc :
-0,5g( xR/(Vo*cos))2 + xR tan + zP = xR tan
+ zP = xR tan
C'est un trinôme du second degré...
Non, j'ai perdu le - en route  ... Excuse...
... Excuse...
Nous avons donc :
zR = -0,5g( xR/(Vo*cos))2 + xR tan + zP
+ zP
et, d'autre part, :
zR = -xR tan
Donc : -0,5g( xR/(Vo*cos))2 + xR tan + zP = -xR tan
+ zP = -xR tan
C'est un trinôme du second degré...
Je crois qu'il ne manque rien...
J'ai encore perdu quelque chose... Les copier-coller ne fonctionnent pas bien  ...
...
zR = -0,5g( xR/(Vo*cos ))2 + xR tan
))2 + xR tan + zP
+ zP
donc :
-0,5g( xR/(Vo*cos ))2 + xR tan
))2 + xR tan + zP = -xR tan
+ zP = -xR tan
En espérant n'avoir rien oublié cette fois...
ok!
Merci beaucoup!
Je vais essayer et je vous tiens au courant si le résultat est cohérent ou non 
Encore merci
Quand on a xR et yR, L n'est pas un problème...
L'équation que j'ai écrite (dans laquelle il subsistait une erreur d'ailleurs ! ) :
) :
-(g/(2v02cos2 ))xR2 + xR tan
))xR2 + xR tan + zP = -xR tan
+ zP = -xR tan
donne un trinôme du second degré
Le discriminant est  = (tan
= (tan +tan
+tan )2+(2 zP g / (v0cos
)2+(2 zP g / (v0cos )2)
)2)
Il y a 2 racines dont une négative (qui ne nous intéresse pas)
xR = (tan +tan
+tan +
+
 ) / (g / (v0cos
) / (g / (v0cos )2)
)2)
On trouve xR = 173,343...
et yR = -xR tan = -206,582...
= -206,582...
sauf erreur éventuelle de ma part mais j'ai bien relu...
Equations paramétriques de la trajectoire du sauteur:
x(t) = Vo.cos(alpha).t
z(t) = zo + Vo.sin(alpha).t - gt²/2
x(t) = 25.cos(10°).t
z(t) = 6 + 25.sin(10°).t - 9,8.t²/2
x(t) = 24,62.t
z(t) = 6 + 4,34.t - 4,9.t²
En éliminant t entre ces 2 équations, on a l'équation de la trajectoire du sauteur:
t = x/24,62
z = 6 + 4,34.x/24,62 - 4,9.(x/24,62)²
z = 6 + 0,176.x - 0,008084 x²
Equation du profil de la piste:
z = -tg(50°).x
z = -1,19175.x
Les coordonnées du point d'impact R du skieur au sol sont solutions du système:
z = 6 + 0,176.x - 0,008084 x²
z = -1,19175.x
6 + 0,176.x - 0,008084 x² = -1,19175.x
0,008084 x² - 1,3678 x - 6 = 0 (avex x > 0)
--> x = 173,5 m
z = -1,19175 * 173,5 = -206,7 m
R(173,5 ; -206,7) en m
L = V(173,5² + 206,7²) = 270 m
-----
Ceci évidemment si on peut considérer la trajectoire du skieur comme balistique, ce qui est à 100 lieues de la vérité... Mais c'est une autre histoire.
Sauf distraction. 




