Inscription / Connexion Nouveau Sujet
Travail d'une force
Bonsoir, j'arrive à la fin d'un DM mais je dois avouer que je sèche sur une question en particulier.
Voici d'abord l'énoncé :
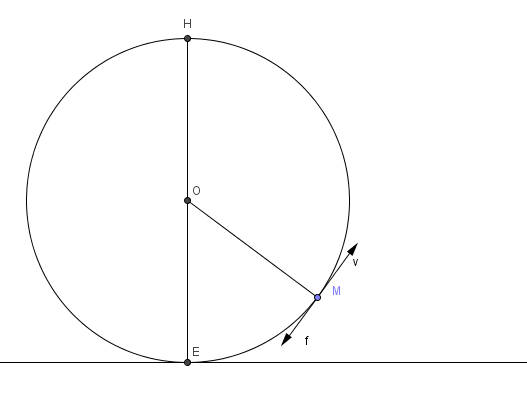
On considère une balançoire de masse nulle, tournant sans frottement autour de son axe O, et au bout de laquelle est attachée un objet de masse m ramené en son centre d'inertie M. La distance OM est notée R. On donne à l'objet à sa position d'équilibre une vitesse initiale horizontale vecteur(vo). On considère le champ de pesanteur g uniforme.
1. Dans un premier temps, on néglige toute action de l'air.
a. Déterminer la position maximale atteinte avec vo=
 (2gR)
(2gR)
b. Déterminer l'expression de vo minimale permettant de monter jusqu'à la position verticale, en supposant que la corde reste tendue jusqu'au bout.
c. Montrer qu'en réalité la corde ne reste pas tendue, et que l'expression attendue à la question précédente est vo=
 (5gR)
(5gR)
2. En réalité, même cette dernière valeur de vo est insuffisante pour arriver à la verticale haute, du fait des frottements. On supposera que l'objet peut être assimilé à une boule de centre M et de rayon r subissant les frottements de l'air selon la loi de Strokes : vecteur(f)=-6

 r
r où vecteur(f) est la force de frottement,
où vecteur(f) est la force de frottement,  la viscosité de l'air et
la viscosité de l'air et  la vitesse de M dans le référentiel terrestre.
la vitesse de M dans le référentiel terrestre.
a. Déterminer un majorant de f (norme) au cours du mouvement de M jusqu'en haut, puis un majorant de la valeur absolue du travail des frottements de l'air.
b. Proposer alors une expression de vo minimale permettant de monter jusqu'en haut.
J'en suis à la question 2. a. où il faut trouver le majorant du travail des frottements de l'air.
Pour la première partie de la question, j'ai dit que f était la plus grande quand v est la plus grande, soit quand on a f=6

 rvo ; donc un majorant de f est tel que f
rvo ; donc un majorant de f est tel que f  6
6
 rvo. Je ne vois pas comment trouver un majorant du travail puisque les expression que l'on connait ne sont valides que dans le cas d'une force constante, ce qui n'est pas le cas ici... Je sais qu'on peut exprimer le travail dans le cas général avec les intégrales, mais ce n'est pas du niveau terminale.
rvo. Je ne vois pas comment trouver un majorant du travail puisque les expression que l'on connait ne sont valides que dans le cas d'une force constante, ce qui n'est pas le cas ici... Je sais qu'on peut exprimer le travail dans le cas général avec les intégrales, mais ce n'est pas du niveau terminale.
Merci d'avance pour votre aide.
bonjour,
donc un majorant de f est tel que f < 6

 rvo
rvodonc un majorant de f (en module) est 6

 rvo
rvo
f < fo => |Wf| < |Wfo|
on calcule doncle travail de ce majorant de f et comme ce majorant est une constante...
Je vois, mais pour calculer ce |Wfo| que doit on faire ?
Est-ce qu'on a |Wfo| = EH*6
 rvo*cos
rvo*cos avec
avec  l'angle entre EH et fo ? Si oui, c'est un angle droit donc le cosinus est égal à 0 et le travail est nul...
l'angle entre EH et fo ? Si oui, c'est un angle droit donc le cosinus est égal à 0 et le travail est nul...
non, le point M parcourt l'arc EH pas le segment [EH]
et la force de frottement f est toujours colinéaire à  donc au déplacement dl
donc au déplacement dl
Wfo= fo =
 R fo
R fo
Ah oui, c'est vrai que ce n'est pas une pente droite ! Merci.
Donc on a Wfo = fo = 6
 ²
² rRvo
rRvo
Ainsi, dans la question suivant, on utilise le théorème de l'énergie mécanique :
Em(E)-Em(H)  Wfo ?
Wfo ?
oui mais il faut expliquer pourquoi
le théorème de l'énergie mécanique donne ici entre E et H: Em(H) - Em(E) = - |Wf| <0
donc effectivement: Em(E) - Em(H) = |Wf| < |Wfo|
Seulement, à partir de Em(E) - Em(H) < |Wfo| on obtient (1/2)mvo²-mg2R < |-6 ²
² rvo| ; on ne peut pas isoler vo ou alors on résout une inéquation du second degré avec vo en inconnu, mais ça me semble quelque peu hors sujet.
rvo| ; on ne peut pas isoler vo ou alors on résout une inéquation du second degré avec vo en inconnu, mais ça me semble quelque peu hors sujet.
mais ça me semble quelque peu hors sujet.
c'est au programme donc je ne vois pas ce qui te gêne.
a priori, avec le majorant que tu as pris, il faut résoudre:
Vo2 = 5gR + 2 |Wfo|/m
<=> Vo2 - KVo - 5gR = 0 avec K = 12
 2
2 rR/m
rR/m
sauf erreur
|Wf| < 6.Pi.eta.r.Vo * Pi.R
|Wf| < 6.Pi².eta.r.R.Vo
1/2 m.Vo² - 6.Pi².eta.r.R.Vo - mg.2R = 1/2.m.VH²
Or on doit avoir m .VH²/R >= m.g (pour que la ficelle reste tendue en H)
VH² >= g.R
1/2 m.Vo² - 6.Pi².eta.r.R.Vo - mg.2R = 1/2.m.g.R
m.Vo² - 12.Pi².eta.r.R.Vo - mg.4R = m.g.R
m.Vo² - 12.Pi².eta.r.R.Vo - 5.m.g.R = 0
Vo² - (12.Pi².eta.r.R/m).Vo - 5.g.R = 0
Vo = (6.Pi².eta.r.R/m) + RC[(6.Pi².eta.r.R/m)² + 5g.R]
C'est Vo min pour "monter jusqu'en haut" ... si le module de la force de frottement restait constant et égal à celui en H pendant tout le parcours EH.
En réalité Vo min est un peu plus petite que celle calculée puisque la vitesse diminue en cours du trajet EH.... Ce calcul n'est pas demandé.
-----
Sauf distraction. 
Je corrige quand même une distraction de ma part.
Lire : "C'est Vo min pour "monter jusqu'en haut" ... si le module de la force de frottement restait constant et égal à celui en pendant tout le parcours EH. "

Bonjour ; merci énormément à vous deux, je dois bien avouer que je n'en attendais pas autant (notamment au niveau de la résolution de l'équation, je suis surpris que vous la donniez, mais ça me permet de me vérifier) ! Il reste quelques questions ensuite mais je saurai me débrouiller.
c'est au programme donc je ne vois pas ce qui te gêne.
C'est le résultat que je trouvais qui me semblait étrange, mais il me manquait une partie du raisonnement (la vitesse en H pour que la corde soit tendue, pourquoi n'y ai-je pas pensé sachant que c'est la question 1. c ...) donc je n'avais qu'une partie de la racine de juste.
Encore merci




