voila le schéma de la situation sa peut peut  etre aider à comprendre, en tout cas perso ça ne m'a pas aidé!! merci si vous pouvez m'aider!!

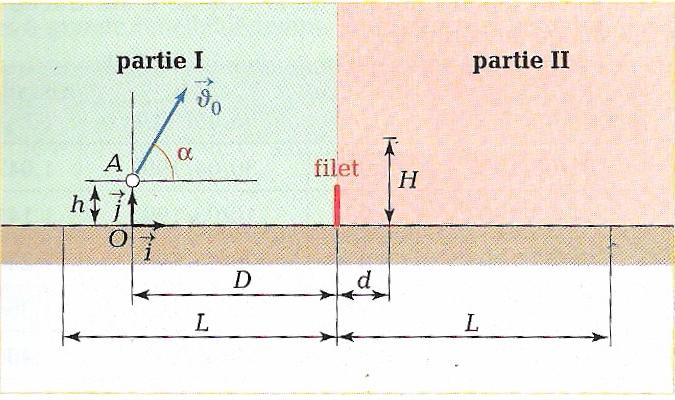
Bonjour,

Je découvre ton schéma au moment de mettre le mien... Va-t-il t'aider davantage ? Il est nettement moins joli, un peu plus "mathématique"...     



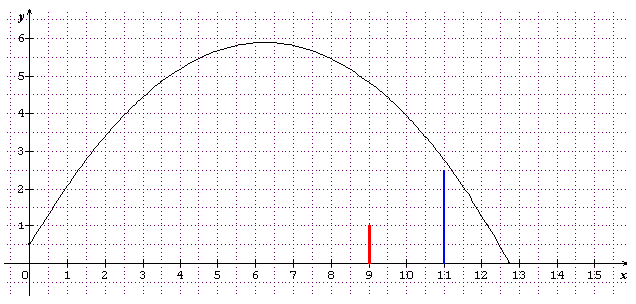
En rouge le filet
La balle part à 9 m du filet et d'une hauteur de 0,5 m
La vitesse au départ fait un angle de 60° avec l'horizontale

Quelle force agit sur la balle "en vol" ?
Quelle relation vectorielle peux-tu écrire ?
Quelles projections de cette relation sur les axes ?
Quelles équations pour décrire le mouvement ?

1) a)

En prenant l'origine des temps au moment où la balle est frappée.

Au départ, la composante horizontale de la vitesse da la balle est Vo.cos(alpha)
Au départ, la composante verticale de la vitesse de la balle est Vo.sin(alpha)

Si on néglige les frottements de la balle dans l'air:
Il n'y a aucune force qui agit horizontalement sur la balle --> la composante horizontale de la vitesse de la balle (notée Vh) reste constante pendant toute la trajectoire de la balle: Vh(t) =  Vo.cos(alpha)

Dans le sens vertical, le poids de la balle agit sur la balle et donc la composante verticale de la vitesse de la balle (notée Vh) sera : Vv(t) = Vo.sin(alpha) - gt

On a Vh(t) = dx(t)/dt et Vv(t) = dy(t)/dt

Par intégration, on trouve donc directement :

x(t) = xo + Vo.cos(alpha).t
y(t) = yo + Vo.sin(alpha).t - gt²/2

Et l'énoncé donne xo = 0 --> x(t) = Vo.cos(alpha).t
t = x/(Vo.cos(alpha))

y(t) = yo + Vo.sin(alpha).x/(Vo.cos(alpha)) - g[x/(Vo.cos(alpha))]²/2

y(t) = yo + x.tg(alpha) - x².g/(2.Vo².cos²(alpha))

C'est l'équation de la trajectoire de la balle (pour x > 0 et pour autant que y reste >=0 et que la balle ne cogne ni le filet ni l'adversaire).
-----
...

Sauf distraction.  

merci beaucoup!! j'ai enfin compris, tous ces sin et cos ça m'embrouille!!
pour la 2 eme question il suffit simplement de remplacer par les valeur ce qu'il y a dans l'équation :y(t) = yo + x.tg(alpha) - x².g/(2.Vo².cos²(alpha))  ? car c'est ce que j'ai fait j'espere que c'est sa!!
merci beaucoup encore!

Bonjour je suis en Term S et il se trouve que j'ai exactement le même sujet en exercice maison et malgré les explications je ne comprend pas la démarche pour répondre à la deuxième question!! Si quelqu'un peut m'aider, je vous remercie!

Bonjour,

Regarde la figure (18/02/2008 à 8h 51) en particulier la trajectoire (en noir) et le trait bleu...
Cela pour l'aspect "qualitatif" de la question.

Quant à l'aspect "quantitatif" tu as les équations et en particulier celle de la trajectoire...

D'accord ?

Heu... Oui je comprend a peu près le schéma mais ce que je n'arrive pas à determiner c'est comment on peut trouver une équation avec y(x) et des valeur numérique alors qu'avant on a trouver à la question précédente y(t).
Je suis vraiment désolé mais ce chapitre j'ai énormement de mal a le comprendre.

Relis le message de J-P

Tu as d'une part la relation entre les hauteurs et le temps y(t)
mais tu as aussi la relation entre les abscisses et le temps x(t)

de cette dernière relation du peux déduire t en fonction de x
et remplacer cette expression de t dans y(t)

tu en déduis y(x)

D'accord!!! Merci beaucoup, ca m'éclaire déjà un peu plus bien que je n'en vois pas l'interet.
Merci a tout le monde pour votre rapidité et vos explications!!!

J'avais écrit l'équation de y(x) ...
Mais j'avais sottement été distrait et l'avait noté y(t) au lieu de y(x)

La fin de mon message aurait du être :

y(x) = yo + x.tg(alpha) - x².g/(2.Vo².cos²(alpha))