Inscription / Connexion Nouveau Sujet
trajectoire d'un électron dans un champ électrostatique
Bonjour, je voudrais savoir si vous pourriez m'aider, j'ai un devoir maison a rendre en physique et je suis bloquée.
On considère un électron de masse m de charge électrique -e, initialement animé d'un mouvement rectiligne uniforme à la vitesse 
1. Il entre au point O dans une région délimitée par 2 grilles horizontales entre lesquelles règne un champ électrostatique uniforme vertical ascendant (vecteur) E. Les 2 grilles sont séparées d'une distance d. On négligera le poids de l'électron.
J'ai réussi à déterminer les équations horaires du mouvement ainsi que l'équation de la trajectoire, il s'égit d'une parabole.
Par contre je bloque à la suite de l'exercice :
3c)Déterminer graphiquement les coordonées du vecteur vitesse S (S étant le somment de la trajectoire)
d) En déduire la date ts à laquelle l'électron atteint le sommet
e) Montrer que S a pour ordonnée zs = (m*(1*cos i1)²) / (2e*E)
4) Quelle est la condition pour sur la valeur E du champ électrostatique pour que l'électron atteigne la région située au dessus de la grille supérieure ?
5a) Si cette condition est remplie, comment qualifier la nature du mouvement dans cette région ? (je pense qu'il s'agira d'un mouvement rectiligne uniforme..)
b) L'électron traverse la grille avec une vitesse 2. On note i2 l'angle entre ce vecteur et la verticale. Exprimer le sinus de l'angle i2 en fonction de v1 v2 et du sinus de l'angle i1
Merci beaucoup d'avance de votre aide
Bonjour à tous les deux,
smilin >>
Pour apprendre à insérer une image, une figure, un schéma, un graphique, un tableau (pas un énoncé !) clique sur la maison 
Il faut d'abord réaliser un fichier qui représente l'image (qui est, en général, sur un livre). Il faut donc utiliser un "scanner".
Il faut cliquer sur l'icône "Img" sous le cadre réponse pour pouvoir sélectionner le fichier. MAIS le fichier doit remplir 2 conditions :
- la taille de l'image ne doit pas être supérieure à 650 x 600 pixels
- la taille du fichier ne doit pas dépasser 40 ko
On peut adapter l'image afin qu'elle respecte ces conditions à l'aide d'un logiciel de traitement d"image. Paint est un logiciel qui est fourni avec Windows et qui peut faire ça. Le format de fichier que je recommande est le format gif (pour la taille du fichier). D'autres logiciels de traitement d'image plus sophistiqués que Paint existent mais certains sont payants et il faut apprendre à les utiliser.
(Gimp est un exemple de logiciel de traitement d'image gratuit. On le trouve sur le net sans problème).
Si l'image ne respecte pas ces deux conditions, il est impossible de l'attacher au message.
Je n'ai pas de scanner chez moi, alors j'ai essayé de reproduire au mieux la figure, j'espère que c'est suffisamment clair..
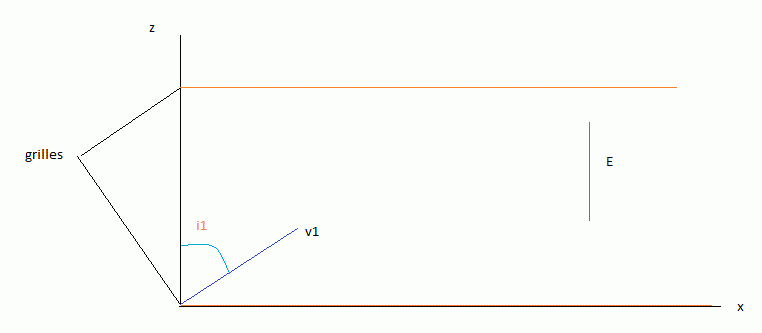
Edit Coll : image recadrée
F = q.E
avec q = -e
F = -e.E = m.a (avec m la masse de l'électron et a l'accélération de l'électron dans la direction du champ).
a = -e.E/m
z(t) = V1.cos(i1).t - e.E/m * t²/2
x(t) = v1.sin(i1).t
------
Sommet atteint pour dz/dt = 0, soit donc :
V1.cos(i1) - t.e.E/m = 0
à l'instant t = mV1.cos(i1)/(e.E) [date à laquelle l'électron atteint le sommet de sa trajectoire).
z(sommet) = V1.cos(i1).mV1.cos(i1)/(e.E) - e.E/m * [mV1.cos(i1)/(e.E)]²/2
z(sommet) = cos²(i1).mV1²/(e.E) - m.V1²/(2.e.E) .cos²(i1)
z(sommet) = (m.v1².cos²(i1))/(2eE)
-----
4)
il faut que d < (m.v1².cos²(i1))/(2eE)
-----
5b)
avec z(t) = d, il vient :
V1.cos(i1).t1 - e.E/m * t1²/2 = d (1)
On peut ainsi calculer la valeur de t1 ... (qui est l'instant où l'électron arrive à la grille supérieure).
On peut ensuite calculer les composantes suivant les axes (ox et oz) de la vitesse de l'électron à l'instant t1.
dx/dt = V1.sin(t)
dz/dt = V1.cos(i1) - e.E/m * t
(dx/dt)(t1) = V1.sin(t1)
(dz/dt)(t1) = V1.cos(i1) - e.E/m * t1
On remplace t1 par ce qui à été trouvé avec (1) ...
Et on peut en déduire sin(i2) = ...
-----
Sauf distraction.
Merci beaucoup !
Pour z(t) et x(t) j'avais trouvé les mêmes résultats
Par contre pour le 5)a), il s'agit bien d'un mouvement rectiligne uniforme ?
Et je n'ai pas très bien compris le 5)b).. Il faut exprimer le sinus de l'angle i2 en fonction de v1, v2 et du sinus de l'angle i1
J'ai oublié de joindre le deuxième schéma, lorsque l'électron traverse la grille supérieure excusez moi :
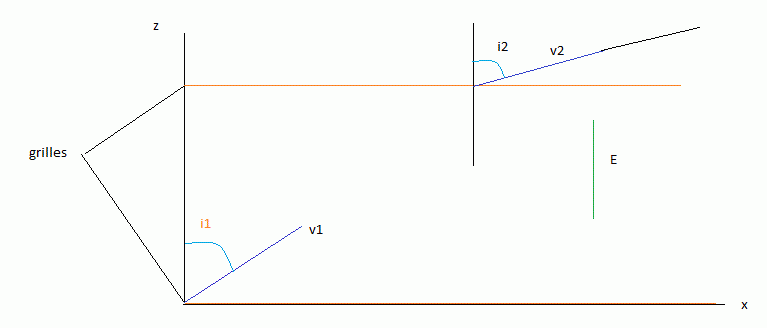
"Par contre pour le 5)a), il s'agit bien d'un mouvement rectiligne uniforme ? " : Oui
et pour l'angle i2 :
Comme je l'ai écrit, on peut facilement calculer les composantes suivant les axes de la vitesse v2.
(Par (dx/dt)(t1) et (dz/dt)(t1) avec les notations de mon précédent message)
Et avec ces 2 composantes, on peut en déduire les fonctions trigonométriques de l'angle i2.
Il y a peut-être d'autres méthodes pour y arriver.
V1.cos(i1).t1 - e.E/m * t1²/2 = d
(e.E/m) * t1² - 2V1.cos(i1).t1 + 2d = 0
Equation du second degré de variable t1.
t1 = [V1.cos(i1) +/- racinecarrée(V1²cos²(i1) - 2deE/m)]/(e.E/m)
C'est la plus petite des 2 solutions qui convient, soit :
t1 = m.[V1.cos(i1) - racinecarrée(V1².cos²(i1) - 2d.e.E/m)]/(e.E)
Sauf erreur ...
Et donc je cherche les composantes de (dx/dt)(t1) et de (dz/dt)(t1) en remplaçant t1 par la valeur trouvée précédemment ?
Annuler
connectez vous