Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Niveau terminale
Partager :

Tension des fils

Posté par
pfff 24-05-20 à 14:02

Bonjour j'aimerais de l'aide pour terminer cet exo.

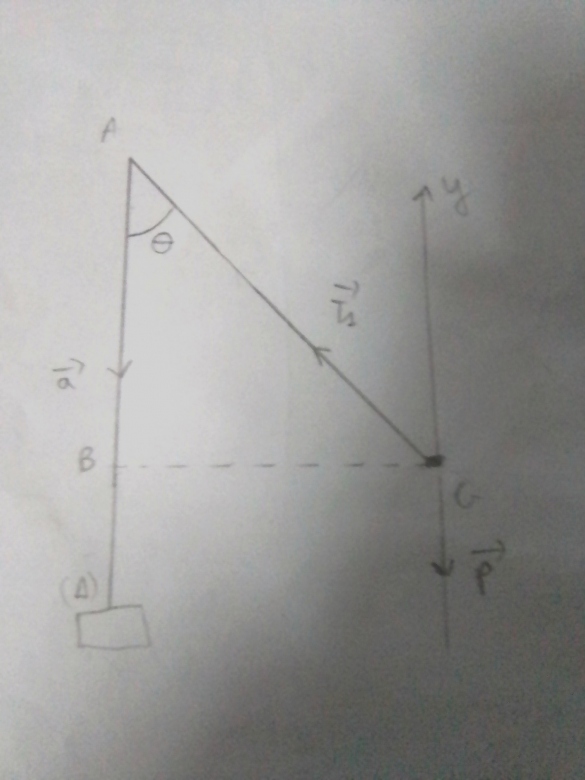
Un solide de masse m=500g est assimilé à son centre d'inertie G. Il est relié aux points A et B par deux fils inextensibles de masses négligeables (Voir figure ). Les fils sont accrochés à un axe vertical, solidaire d'un moteur qui entraîne le solide  dans un mouvement de rotation, à la vitesse angulaire constante. Soit \vec{T_1} la tension du fil AG et \vec{T_2} la tension du fil BG.
est l'angle entre l'axe et AG. Lorsque le fil BG est tendu, il est alors perpendiculaire à .
La longueur de AG = l = 50cm. La longueur du fil BG est l'=43,30cm. On donne l'intensité du champ de pesanteur g=10m.s^-^2.

1. Etude du système lorsque le fil BG n'est pas tendu.

1-1- Donner la valeur de l'angle lorsque = 0. Déterminer alors la tension T_1 du fil.
Je sais que \large \omega = \frac{d\theta }{dt} mais je ne vois pas comment déterminer .

1-2- La vitesse angulaire du solide 0.

1-2-1- En appliquant le théorème du centre d'inertie au solide, dans le repère (C ; x ; y ), établir que cos\theta = \dfrac{g}{l\omega² }.
On remarquera que les coordonnées du vecteur accélération sont : a_x=-a_o et a_y = 0 et le rayon de la trajectoire r=BG

1-2-2- En déduire que le solide G ne s'écarte de l'axe , que si \omega \geq \omega_o = \sqrt{g/l}

1-2-3- Déterminer lorsque < \omega_1
, la tension T_1 du fil AG.

1.3 On considère que > \omega_1

1-3-1- Pour quelle valeur \theta_1 de l'angle le fil BG commence à se tendre.

1-3-2- Calculer la vitesse angulaire \omega_1 du solide si =\theta_1 ; le fil BG étant toujours considéré non tendu.

2. Etude du système lorsque le fil BG est tendu.
La vitesse angulaire du solide est telle que > \omega_1

2-1- Quelle est la valeur de l'angle ?

2-2- Déterminer les tensions T_1 et T_2 des fils lorsque = 10 rad.s^-^1


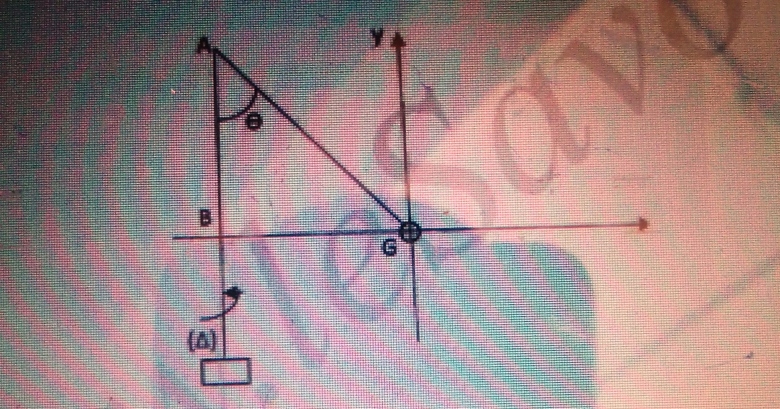
Tension des fils


Je bloque dès la question 1 . Merci de m'aider.

Posté par
vanoisere : Tension des fils 24-05-20 à 14:50

Bonjour
Tu commences par une énorme confusion ; Il existe des problèmes où on définit la vitesse angulaire comme la dérivée de par rapport à t mais ici est l'angle d'inclinaison du fil considéré comme une constante !
Il faut appliquer la relation fondamentale de la dynamique à la masse ; cela suppose de connaître l'expression de l'accélération dans le cas d'un mouvement circulaire uniforme.

Posté par
pfffre : Tension des fils 24-05-20 à 14:51

a=v²/r

C'est cela ?

Posté par
vanoisere : Tension des fils 24-05-20 à 15:21

Oui ; ou encore : a=r.2 puisque : v=r.
Il te faut faire un schéma clair avec les différents vecteurs force en supposant, pour la première partie, que le fil BG ne joue aucun rôle.

Posté par
pfffre : Tension des fils 24-05-20 à 15:47

ok.

Si le fil BC ne joue aucun rôle dois je donc le faire horizontal ?

Posté par
pfffre : Tension des fils 24-05-20 à 15:50

a = r²   or = 0

donc a = 0m/s²

maintenant comment je détermine T_1 ?

Posté par
pfffre : Tension des fils 24-05-20 à 15:51

Citation :
Si le fil BG ne joue aucun rôle dois je donc le faire horizontal ?

Posté par
vanoisere : Tension des fils 24-05-20 à 15:56

Tant que le fil BG n'est pas tendu, il n'exerce aucune force. Tu peux donc faire un schéma sans le représenter.

Posté par
pfffre : Tension des fils 24-05-20 à 15:57

pfff @ 24-05-2020 à 15:50

a = r²   or = 0

donc a = 0m/s²

maintenant comment je détermine T_1 ?


J'oubliais comment je détermine d'abord

Posté par
pfffre : Tension des fils 24-05-20 à 15:57

pfff @ 24-05-2020 à 15:50

a = r²   or = 0

donc a = 0m/s²

maintenant comment je détermine T_1 ?


J'oubliais comment je détermine d'abord

Posté par
vanoisere : Tension des fils 24-05-20 à 15:58

Dans le cas où le système ne tourne pas, tu as effectivement une accélération nulle. Le fil se contente de compenser le poids...

Posté par
pfffre : Tension des fils 24-05-20 à 16:07

Voila

Tension des fils

Posté par
vanoisere : Tension des fils 24-05-20 à 16:09

C'est correct. Applique la relation fondamentale de la dynamique (deuxième loi de Newton) et projette-là sur deux axes : un horizontal et un vertical.

Il serait aussi utile de représenter le vecteur accélération sur le schéma.

Posté par
pfffre : Tension des fils 24-05-20 à 16:27

donc

\sum{_\vec{F_ext}} = \vec{0} \Leftrightarrow \vec{P} + \vec{T_1} = \vec{0}

lorsqu'on projette sur (y'y) on obtiens -P  + T_1Cos= 0 -mg + T_1Cos =0
( on cherche bien sur mais il y'a T_1 dans la relation c'est pour ça que je ne vois pas comment continuer )

pour l'axe vertical je ne vois pas puisqu'on n'a plus (x'x)

Posté par
pfffre : Tension des fils 24-05-20 à 16:28

Tension des fils

Posté par
vanoisere : Tension des fils 24-05-20 à 18:25

Dans le cas où le système ne tourne pas (=0), l'immobilité de la masse dans le repère terrestre considéré comme galiléen conduit simplement à :

\overrightarrow{P}+\overrightarrow{T}=\overrightarrow{0}\quad donc\quad\overrightarrow{T}=-\overrightarrow{P}

Le vecteur poids étant vertical descendant, le vecteur tension est vertical ascendant : le fil pend verticalement le long de l'axe ( ). L'angle est nul !

Pour le cas d'une vitesse angulaire non nulle, il faut faire une figure propre avec les vecteurs forces et le vecteur accélération. Le mouvement de M est un mouvement circulaire de rayon BG et de centre B. L'accélération est normale centripète. Je te laisse continuer et faire une figure propre...

Posté par
pfffre : Tension des fils 24-05-20 à 18:47

Citation :
1-1- Donner la valeur de l'angle lorsque = 0.
Déterminer alors la tension T_1 du fil.


Pour déterminer T_1

\quad\overrightarrow{T}=-\overrightarrow{P}


en projetant sur l'axe (y'y) on obtiens T_1 = mg
                                                                                    T_1 = 5 N

c'est cela ?

Posté par
pfffre : Tension des fils 24-05-20 à 19:37

Citation :
Le mouvement de M est un mouvement circulaire de rayon BG et de centre B.


Mais le fil BG n'est toujours pas tendu donc je ne vois pas ou dois être le centre B.

Posté par
vanoisere : Tension des fils 24-05-20 à 21:33

C'est une façon simple à partir d'une figure déjà faite, d'expliquer  que le centre de la trajectoire circulaire est le projeté orthogonal de G  sur l'axe vertical de rotation, que le fil soit tendu ou pas.

Posté par
pfffre : Tension des fils 24-05-20 à 21:55

Ok. Mais vous n'avez pas donné votre avis pour le T_1 que j'ai trouvé.

Citation :
1-2-1- En appliquant le théorème du centre d'inertie au solide, dans le repère (C ; x ; y ), établir que cos\theta = \dfrac{g}{l\omega² }.
On remarquera que les coordonnées du vecteur accélération sont : a_x=-a_o et a_y = 0 et le rayon de la trajectoire r=BG


donc on a : \sum{_\vec{F_ext}} = \vec{ma} \Leftrightarrow \vec{P} + \vec{T_1} = \vec{ma}


. Sur l'axe (y'y) : - P + T_1Cos\theta = 0 \: car \: a_y = 0

Pour le premier axe c'est bon ?

Posté par
vanoisere : Tension des fils 24-05-20 à 22:01

Ok.

Posté par
pfffre : Tension des fils 24-05-20 à 22:05

............
Je suis perdu le ''Ok'', c'est pour mon T_1 ou pour mon premier axe ?

Bon si c'est Ok pour mon premier axe, pour le 2e c'est à dire (x'x) je suis un peu perdu.

Merci de m'aider

Posté par
vanoisere : Tension des fils 24-05-20 à 22:12

Tout est bon pour le moment.  Il faut compléter le schéma en y plaçant le vecteur accélération  puis projeter la relation fondamentale de la dynamique sur l'axe horizontal.

Posté par
pfffre : Tension des fils 24-05-20 à 22:49

ok

Tension des fils

j'obtiens sur (x'x) : -T_1 Sin\theta = ma_o \: car\: a_x = a_o

C'est ca ?

Posté par
pfffre : Tension des fils 24-05-20 à 22:55

pfff @ 24-05-2020 à 22:49

ok

j'obtiens sur (x'x) : -T_1 Sin\theta = - ma_o \: car\: a_x = - a_o

C'est ca ?

J'ai rectifié c'est plutot a_x = - a_o

donc on obtiens : T_1 Sin\theta = ma_o

Posté par
vanoisere : Tension des fils 24-05-20 à 23:42

Grâce à un énoncé qui "aide" beaucoup, tu écris la bonne relation mais, à en croire la représentation du vecteur accélération que tu fournis, sans vraiment comprendre...
Il s'agit d'étudier le mouvement du point G, le point A est fixe. G tourne autour de l'axe () sur un cercle de centre B, ce cercle appartenant à un plan horizontal. Le vecteur accélération de G est normale centripète donc orienté de G vers B. Sa norme est r.2 avec r : distance de B à G.

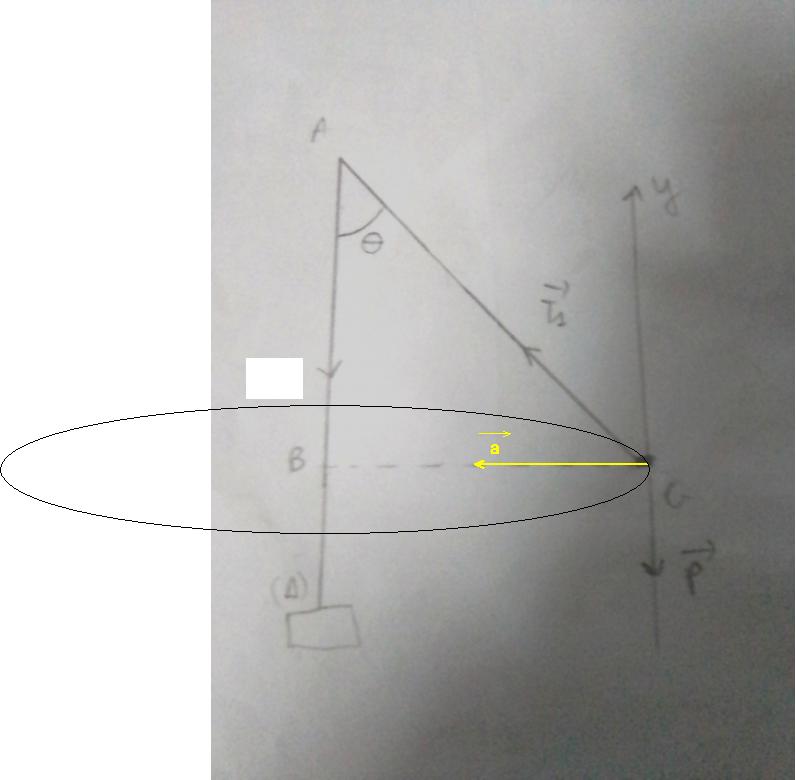
Tension des fils

Posté par
pfffre : Tension des fils 24-05-20 à 23:46

D'accord

Posté par
pfffre : Tension des fils 24-05-20 à 23:50

donc

sur (y'y) on a : T_1 Cos = mg

sur (x'x) on a T_1 Sin  = v.r.²

je vois pas comment trouver cos\theta = \dfrac{g}{l\omega² }

Posté par
pfffre : Tension des fils 25-05-20 à 01:29

Bon j'ai cherché et j'ai vu ça :

on a T_1 Sin  = v.r.² or Sin\theta = \frac{r}{l} \: avec \: l = AG

Donc on a T_1\dfrac{r}{l} = v.r.\omega² \Rightarrow T_1 = v.l.w²

en remplaçant T_1 dans la première égalité, j'obtiens v.l.w² Cos\theta = mg \Rightarrow Cos\theta = \dfrac{mg}{v.l.w²}

Je pensais avoir trouvé mais il n'y a pas de m et de v dans l'expression, et je ne sais pas comment les ôter.

Posté par
vanoisere : Tension des fils 25-05-20 à 11:58

Projection sur (y'y) : d'accord avec toi : T_{1}.\cos\left(\theta\right)=m.g

Projection sur (x'x) : T_{1}.\sin\left(\theta\right)=m.a=m.r.\omega^{2}

Division membre à membre pour faire disparaître T1 du calcul :

\dfrac{\cos\left(\theta\right)}{\sin\left(\theta\right)}=\dfrac{g}{r.\omega^{2}}

En considérant le triangle rectangle (ABG) :

\sin\left(\theta\right)=\dfrac{BG}{AG}=\dfrac{r}{l}

Je te laisse continuer...

Posté par
pfffre : Tension des fils 25-05-20 à 15:20

Merci j'ai vu ou j'avais fait l'erreur j'ai oublié la masse qui précède l'accélération.

Effectivement ça passe.

Posté par
pfffre : Tension des fils 25-05-20 à 15:36

Citation :
1-2-2- En déduire que le solide G ne s'écarte de l'axe , que si \omega \geq \omega_o = \sqrt{g/l}


Je ne comprends pas trop bien la question suivante

Posté par
vanoisere : Tension des fils 25-05-20 à 15:37

Tu sais sûrement qu'un cosinus ne peut être supérieur à 1...

Posté par
pfffre : Tension des fils 25-05-20 à 15:40

J'ai vu pour que le solide G s'écarte il faut que cos 1

Posté par
pfffre : Tension des fils 25-05-20 à 15:44

erreur plutôt

-1 < Cos < 1

Posté par
vanoisere : Tension des fils 25-05-20 à 18:12

Ici, peut varier entre zéro et une valeur maximale inférieure à 90°. Tu as donc :
cos()1
Le cosinus ne peut pas être négatif dans ce problème !

Posté par
pfffre : Tension des fils 25-05-20 à 18:53

Ah d'accord

Posté par
pfffre : Tension des fils 25-05-20 à 18:57

Citation :
          
1-2-3- Déterminer lorsque < \omega_1
, la tension T_1 du fil AG.  


Ici \omega_1 c'est quoi ?

Posté par
vanoisere : Tension des fils 25-05-20 à 19:29

C'est expliqué dans l'énoncé mais un peu plus tard... Pas très logique... Bref :
1 est la valeur particulière de la vitesse angulaire pour laquelle le fil est tendu entre BG sans encore exercer de tension. C'est donc la valeur particulière de pour laquelle r=l'=43,3cm.

Posté par
pfffre : Tension des fils 25-05-20 à 19:49

oups désolé j'ai mal recopié cette partie c'est plutôt :

Citation :
          
1-2-3- Déterminer lorsque < \omega_0
, la tension T_1 du fil AG.  

Posté par
pfffre : Tension des fils 25-05-20 à 19:50

Je dois faire comment ?

Posté par
vanoisere : Tension des fils 25-05-20 à 21:27

Tant que =0, la tension est la même qu'en absence de rotation puisque le fil reste vertical.  D'ailleurs l'énoncé note la tension T1 dans les deux cas.

Posté par
pfffre : Tension des fils 25-05-20 à 22:04

J'ai pas bien compris votre message

le   < \omega_0 ne sert donc à rien ?

Posté par
vanoisere : Tension des fils 25-05-20 à 22:17

Mais si : c'est parce que o que l'on a  : =0 et que le raisonnement de mon message précédent est possible sur  T1.

Posté par
pfffre : Tension des fils 25-05-20 à 22:20

ben c'est qu'on trouve le même T1 que dans la première question  que dans la 1ere question

Posté par
vanoisere : Tension des fils 25-05-20 à 22:26

C'est exactement ce que j'ai déjà expliqué  !

Posté par
pfffre : Tension des fils 25-05-20 à 22:27

j'ai compris maintenant

Posté par
pfffre : Tension des fils 26-05-20 à 15:06

Bonjour vanoise, pour :

Citation :
1.3 On considère que > \omega_o

1-3-1- Pour quelle valeur \theta_1 de l'angle le fil BG commence à se tendre.


J'ai dit il faut que = o

or cos\theta = \dfrac{g}{l\omega² }

donc cos\theta1 = \dfrac{g}{l\omega²_o } et \omega²_o =\frac{g}{l}

je trouve Cos1 = 1 mais je ne sais pas si je dois prendre 1=0 ou 1=90°

Merci de corriger ce que j'ai fait

Posté par
vanoisere : Tension des fils 26-05-20 à 15:11

Tu n'as pas bien compris. J'ai déjà fourni l'explication hier :

Citation :
1 est la valeur particulière de la vitesse angulaire  pour laquelle le fil est tendu entre BG sans encore exercer de tension. C'est donc la valeur particulière de pour laquelle r=l'=43,3cm.

Posté par
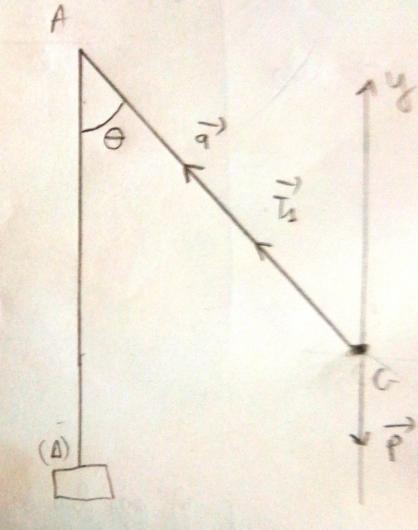
pfffre : Tension des fils 26-05-20 à 15:13

Mais on est pas encore au stade de _1

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !