Inscription / Connexion Nouveau Sujet
Surtension rlc
S'il vous plaît, est ce que quelqu'un peut m'expliquer la surtension en RLC, mon prof l'a expliqué en utilisant les représentations de Fresnel mais je n'ai pas encore imaginé comment on peut avoir une tension au circuit rlc plus grande que la fem du GBF; et aussi comment protéger le circuit contre ce genre de problème ?
Edit Coll : niveau modifié
L'impédance d'une inductance est jwL
L'impédance d'une capacité est -j/(wC)
Donc l'impédance du RLC est : Z = R + j(wL - 1/(wC))
Le courant dans le circuit est : i = Ue/Z (avec Ue la tension délivrée par le GBF)
La tension aux bornes de l'inductance est donc Ul = (jwL) * i
Ul = jwL.Ue/[R + j(wL - 1/(wC))]
En module, on a donc :
|Ul| = |Ue| wL/[racinecarrée(R² + (wL - 1/(wC))²)]
Si on fait varier la fréquence (donc aussi w, on peut arriver à avoir (wL - 1/(wC)) = 0 (pour w = 1/racine(LC))
On a alors : |Ul| = |Ue| wL/[racinecarrée(R²)]
|Ul| = |Ue| wL/R
Et donc si wL > R, on a |ul| > |Ue|, la tension sur L est supérieure à la tension du GBF.
-----
On peut faire un calcul similaire avec la tension sur le condensateur ...
Et montrer qu'à la résonnance, on aura |Ul| = |Ue|/(wRC)
on aura alors |Uc| > |Ue| si : 1/(wC) > R
-----
On remarquera qu'à la résonnance, les conditions wL > R et 1/(wC) > R sont parfaitement les mêmes.
En effet à la résonnace, on a w = 1/racine(LC) --> L = 1/(w²C)
et donc wL > R ---> w*1/(w²C) > R ---> 1/(wC) > R
-----
Donc, à la résonnance on a w = 1/rac(LC), on montre que |Uc| = |Ul|
et si on a wL > R, on a forcément aussi 1/(wC) > R et les tensions |Uc| et |Ul| sont > que la tension du GBF.
-----
A la résonnance, les tensions Ul et Uc ont même amplitude et sont de signes opposés (on a Ul = -Uc)
Dit autrement, à la résonnance, les impédances du L et du C sont égales et opposées, donc leur somme est nulle.
Le courant dans le circuit n'est alors limité que par la résistance...
Et il peut y avoir des "surtensions" sur l'industance et sur le condensateur. (si wL > R, qui est analogue à 1/(wC) > R)
-----
Compris ?

Un peu, j'ai saisi le développement mathématique mais j'ai des lacunes en ce qui concerne la notation complexe,(retard en cours) si tu utilise la notation des fonctions trigonométriques ça sera mieux si possible. Mais j'ai des questions, est ce que la surtension ne peut arriver qu'en résonance ou même en déphasage? Et donc selon ce phénomène de surtension on peut mesurer la tension efficace du Condensateur et de la bobine à chaque moment et voir une tension supérieure à celle du GBF ?
Les surtensions éventuelles sont maximales à la résonnance, mais existe évidemment près de la résonnance.
On a :
|Ul|/|Ue| = wL/[racinecarrée(R² + (wL - 1/(wC))²)]
Ce rapport est évidemment maximum pour wL - 1/(wC) = 0, donc à la résonnance (w = 1/Racine(LC))
Ce rapport est > 1 si wL = 1/(wC) > R
Mais, pour w proche de 1/V(LC), le rapport peut aussi être > 1 (mais de toute manière inférieur à la valeur à la résonnance)
Prenons un cas numérique concret :
L = 10^-3 H
C = 10^-6 F
R = 5 ohms
On calcule :
|Ul|/|Ue| = wL/[racinecarrée(R² + (wL - 1/(wC))²)]
|Ul|/|Ue| = 10^-3.w/[racinecarrée(5² + (10^-3.w - 10^6/w)²)]
C'est le rapport entre les amplitudes de la tension sur l'inductance L et la tension du GBF
Si on entre cette fonction dans une calculatrice graphique, on obtient ceci :
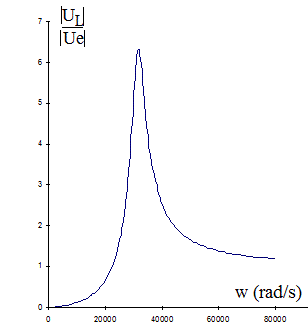
On voit que le rapport est max pour w = 1/racine(LC) = 31623 rad/s (soit f = 31623/(2Pi) = 5033 Hz)
et le rapport vaut alors : wL/R = 31623*10^-3/5 = 6,32
La tension sur l'inductance vaut 6,32 fois celle du GBF.
Mais, aux "alentours" de 31623 rad/s, le rapport reste supérieur à 1 (mais < 6,32 dans l'exemple choisi).
Par exemple il est de 2 vers w = 26000 rad/s et vers w = 45000 rad/s
Il devient < 1 pour w < 22500 rad/s (environ)
Ce rapport tend vers 1 lors w devient très grand ... ce qui est normal parce que à très haute fréquence l'impédance (wL) de l'inductance est beaucoup plus grande que celle du R et que celle du condensateur... et que donc la tension du GBF est presque celle sur l'inductance.
----
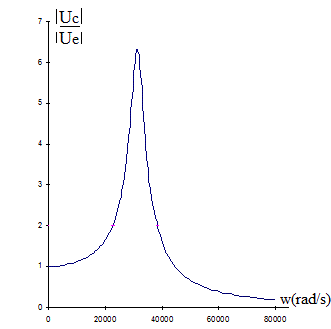
Tu peux essayer de refaire l'exercice avec le rapport |Uc|/|Ue|
on trouve ceci :
...



