Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Sujet Kiné Nantes 2004
Posté par schauch
Bonjour,
Citation :
D'apres Chimix :
:
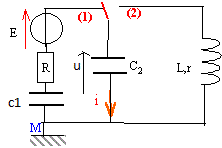
Le générateur est une source de tension idéale de fem E. Les condensateurs ont les capacités C1=C0 et C2 = 2 C0. Initialement le commutateur est en position 1 et les condensateurs sont déchargés.
A t=0 on bascule le commutateur en position 1. Les charges des condensateurs sont à chaque instant égale q1=q2 = q. Justifier.
- Etablir l'équation différentielle vérifiée par la tension u aux bornes du condensateur de capacité C2.
- Quelle est la tension U0 aux bornes du condensateur de capacité C2 quand les charges sont terminées ?
- En fonction de C0 et E exprimer alors la quantité d'électricité Q0 débitée par le générateur, l'énergie EG fournie par le générateur, les énergie EC1 et EC2 stockées par les condensateurs.
- Que représente la différence EJ= EG -(EC1+ EC2 ) ?
- Calculer le rendement énergétique de cette charge (EC1+ EC2 )/EG
- Vérifier que u(t) = U0(1-e-t/t) est solution de l'équation différentielle établie ci-dessus et en déduire l'expression de t en fonction de R et C0. Exprimer an fonction de t la durée nécessaire pour que la charge des condensateurs soit terminée ( on considère que la charge est terminée quand u>=0,99U0)
La charge étant terminée on bascule le commutateur en position 2 et on choisit cet instant comme nouvelle origine des temps.
- On suppose la résistance r de la bobine comme négligeable, établir l'équation différentielle vérifiée par la tension u.
- Calculer la période propre T0 des oscillations.C0=10 mF et L= 0,5 H.
- Etablir l'expression de u(t) et tracer u en fonction de t.
- En réalité l'oscillogramme est celui représenté ci-dessous. Mesurer sur l'oscillogramme la pseudo-période T; la comparer à T0 et conclure.
D'apres Chimix
Le générateur est une source de tension idéale de fem E. Les condensateurs ont les capacités C1=C0 et C2 = 2 C0. Initialement le commutateur est en position 1 et les condensateurs sont déchargés.
A t=0 on bascule le commutateur en position 1. Les charges des condensateurs sont à chaque instant égale q1=q2 = q. Justifier.
- Etablir l'équation différentielle vérifiée par la tension u aux bornes du condensateur de capacité C2.
- Quelle est la tension U0 aux bornes du condensateur de capacité C2 quand les charges sont terminées ?
- En fonction de C0 et E exprimer alors la quantité d'électricité Q0 débitée par le générateur, l'énergie EG fournie par le générateur, les énergie EC1 et EC2 stockées par les condensateurs.
- Que représente la différence EJ= EG -(EC1+ EC2 ) ?
- Calculer le rendement énergétique de cette charge (EC1+ EC2 )/EG
- Vérifier que u(t) = U0(1-e-t/t) est solution de l'équation différentielle établie ci-dessus et en déduire l'expression de t en fonction de R et C0. Exprimer an fonction de t la durée nécessaire pour que la charge des condensateurs soit terminée ( on considère que la charge est terminée quand u>=0,99U0)
La charge étant terminée on bascule le commutateur en position 2 et on choisit cet instant comme nouvelle origine des temps.
- On suppose la résistance r de la bobine comme négligeable, établir l'équation différentielle vérifiée par la tension u.
- Calculer la période propre T0 des oscillations.C0=10 mF et L= 0,5 H.
- Etablir l'expression de u(t) et tracer u en fonction de t.
- En réalité l'oscillogramme est celui représenté ci-dessous. Mesurer sur l'oscillogramme la pseudo-période T; la comparer à T0 et conclure.
A la question
Citation :
Etablir l'équation différentielle vérifiée par la tension u aux bornes du condensateur de capacité C2
Etablir l'équation différentielle vérifiée par la tension u aux bornes du condensateur de capacité C2
chimix avance
Citation :
u' +1/ t u =1,5 E/(RC0) avec
u =1,5 E/(RC0) avec  = 2/3RC0.
= 2/3RC0.
u' +1/ t
 u =1,5 E/(RC0) avec
u =1,5 E/(RC0) avec  = 2/3RC0.
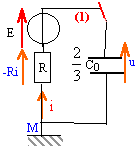
= 2/3RC0.en posant un circuit equivalent avec un condo equivalent C= 2/3 C0
et en posant sur le schema u = tension au bornes du condensateur equivalent
or pour moi la question est de determiner l'equa diff pour verifiée par u aux bornes de C2
j'arrive donc a une equa diff
3E/2RC0 = u' ! 9u/2RC0
et pour moi u correspond a la tension aux bornes de C2. (comme c'est montré sur le schema en bas)
Qui a tord qui a raison?
merci
désolé il y a quelques erreurs d'inattention .
3E/2RC0 = u' + 9u/2RC0
et u' + u/ = 1,5 E/(RC0) avec
= 1,5 E/(RC0) avec  = 2/3RC0.
= 2/3RC0.
apres encore une tentative j'arrive à
E/2RCo= u' +3U/2RCo
ce qui a l'air d'etre en accord avec ta solution.
mon erreur venait du fait que je replacait C par Ceq au lieu de C2...
Merci a toi


