Inscription / Connexion Nouveau Sujet
Statique chez un kinésithérapeute
Bonjour, j'ai plusieurs problème avec cet exercice je viens donc demander votre aide. Merci d'avance 
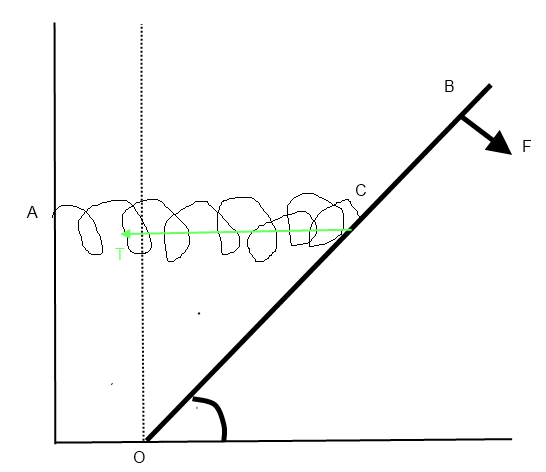
Vous exercez une force F sur la barre OB de longueur L ( F  OB ) qui peut tourner sans frottement autour du point O. La barre OB est retenue par un ressort de raideur k attaché en A et en C milieu de OB. Il y a une glissière ( verticale ) sur le mur au point A de sorte que la direction AC du ressort est toujours horizontale quelque soit l'orientation de OB. Le ressort n'exerce plus aucune force lorsque la barre OB est verticale ( le long du pointillé vertical partant de O )
OB ) qui peut tourner sans frottement autour du point O. La barre OB est retenue par un ressort de raideur k attaché en A et en C milieu de OB. Il y a une glissière ( verticale ) sur le mur au point A de sorte que la direction AC du ressort est toujours horizontale quelque soit l'orientation de OB. Le ressort n'exerce plus aucune force lorsque la barre OB est verticale ( le long du pointillé vertical partant de O )
1. Représentez sur un dessin l'ensemble des forces agissant sur la tige OB. On négligera dans ce qui suit le poids de la barre devant les autres forces.
Pour le bilan des forces j'ai mis la tension exercée par le ressort, le poids est négligeable et la force F énoncée.
2. Calculez le moment des forces au point O. Ecrire les conditions d'équilibre statique et en déduire comment varie le module de la force F en fonction de l'inclinaison  de la tige. Etudiez la fonction F(
de la tige. Etudiez la fonction F( ) et trcez son graphe pour 0<
) et trcez son graphe pour 0< <
< /2 [ Aide : sin2
/2 [ Aide : sin2 =2sin
=2sin cos
cos ]
]
Commentez le résultat. Le kiné ne veut pas que la force F dépasse un maximum de 100N. Comment doit il choisir la constante de raideur du ressort k ( prendre L=1m ) ?
On a un équilibre : 
 =0
=0
J'ai  (OC/T)+
(OC/T)+ (OB/F)=0 mais pour continuer je voudrais déjà être sûre que je n'ai pas oublié de force ?
(OB/F)=0 mais pour continuer je voudrais déjà être sûre que je n'ai pas oublié de force ?
3. Déterminez les composantes horizontales et verticales de la réaction du sol appliquée en O sur la barre OB.
bonsoir,
je voudrais déjà être sûre que je n'ai pas oublié de force ?
si tu lis attentivement l'enoncé jusqu'au bout tu va voir qu'il en manque une!
Non non c'est exact la réaction du support sur la barre.
Je calcule le moment des forces au point O :
 (OB
(OB F)+(OC
F)+(OC T)=0 et
T)=0 et  (N/O)=0
(N/O)=0
C'est tout ce que j'ai à répondre pour "calculez le moment des forces en O" ?
Je n'arrive pas très bien avec les histoires de moment.
Je crois qu'on a -OB*F-OC*T=0 car F(-j) et T opposé sens repère.
il vaut mieux utiliser la formule : |M|= |F|.d avec d: bras de levier
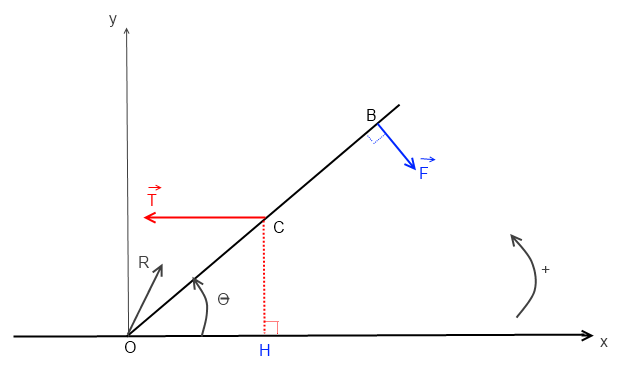
ici (cf figure):
M R/O = 0
M F/O = - |F| . OB = - FL
M T/O = + |T| . CH
et CH peut s'exprimer en fct de OC et de 
quant à |T| on peut l'exprimer en fonction de k et de l'allongement du ressort
comme  M = 0 à l'equilibre, on en déduit F(
M = 0 à l'equilibre, on en déduit F( )
)
sauf erreur
Je ne comprends pas très bien le T*CH, c'est une projection j'imagine mais j'ai du mal avec ça, pouvez vous m'expliquer ?
Sinon je trouve CH=sin *OC et T=-kx
*OC et T=-kx
Donc  M=-FL-kx(sin
M=-FL-kx(sin OC)=0
OC)=0
J'en déduit F( )=kx(sin
)=kx(sin OC)/L
OC)/L
Sinon l'angle va de 0 à 90° donc sin0<sin <sin
<sin /2
/2
soit 0<sin <1 donc pour
<1 donc pour  =0 F est nulle et pour
=0 F est nulle et pour  =
= /2 La force F=kxOC/L
/2 La force F=kxOC/L
Mais je ne vois pas comment tracer un graphe avec ça ?
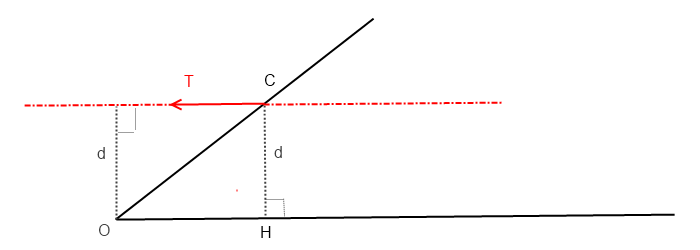
on a: |M|= |F|.d avec d: bras de levier
et le bras de levier, ici, c'est la distance de O à la droite d'action de la force
donc pour T on a la situation indiquée plus bas sur la figure.
d'autre part: OC = L/2 et T = -kx
or
Le ressort n'exerce plus aucune force lorsque la barre OB est verticale
donc l'allongement x est connu: c'est OH (à exprimer en fct de L et de l'angle
 )
)
Oui je vois mais ce que j'avais marqué avant est bon ?
Du coup j'ai -FL-k(cos *L/2)(sin
*L/2)(sin *L/2)=0 C'est bon ?
*L/2)=0 C'est bon ?
presque!
le moment de F est négatif
celui de T est positif (si on oriente  comme je l'ai fait)
comme je l'ai fait)
donc c'est: -FL + kL sin  cos
cos  /4 = 0
/4 = 0
Oui du coup je trouve F (theta)= k/4 (sin2theta) mais poire le graphe je n'y arrive pas du tout ! Je sais que sin0=0 Sinpi/2=1...


