Inscription / Connexion Nouveau Sujet
Son, musique et incertitude
Bonjour j'aimerais avoir de l'aide (beaucoup) pour cet exercice :
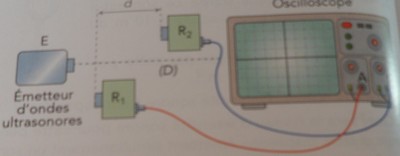
On souhaite connaitre la vitesse d'une onde ultrasonore. La base de temps est fixée à 5,0 s/division; les sensibilités verticales sont identiques. Lorsque les récepteurs sont à égale distance de l'émetteur, les signaux sont en phase. Le récepteur R1 restant fixe, on éloigne le récepteur R2 le long de l'axe (D) en comptant le nombre de fois où les signaux se retrouvent en phase. Pour une distance d égale à (8,5
s/division; les sensibilités verticales sont identiques. Lorsque les récepteurs sont à égale distance de l'émetteur, les signaux sont en phase. Le récepteur R1 restant fixe, on éloigne le récepteur R2 le long de l'axe (D) en comptant le nombre de fois où les signaux se retrouvent en phase. Pour une distance d égale à (8,5 0,1)cm, les signaux ont été dix fois en phase. On considère que l'incertitude U(T) dans la mesure de la période est de 0,2 division. L'incertitude sur la vitesse v est donnée par : U(v)=v.
0,1)cm, les signaux ont été dix fois en phase. On considère que l'incertitude U(T) dans la mesure de la période est de 0,2 division. L'incertitude sur la vitesse v est donnée par : U(v)=v. ((U(
((U( )/
)/ )²+((U(T)/T)².
)²+((U(T)/T)².
a) Calculer la période T des ondes ultrasonores à partir de l'oscillogramme.
b) calculer l'incertitude U(T) sur la période
c) Déterminer la longeur d'onde  connaissant d. Quelle est l'incertitude U(
connaissant d. Quelle est l'incertitude U( ) sur la longueur d'onde ?
) sur la longueur d'onde ?
d) Quelle est la relation entre la longueur d'onde  et la période T de l'onde ?
et la période T de l'onde ?
e) Calculer la valeur de la vitesse v de l'onde ultrasonore et son incertitude U(v).
j'ai fait :
a) TA=3,2.10-5s et TB=3,2.10-5s
b)
je ne sais pas pour toutes les autres merci de bien vouloir m'aider
Bonsoir,
a) Calculer la période T des ondes ultrasonores à partir de l'oscillogramme.
Si tu ne sais pas faire, cela consiste à compter le nombre de divisions entre deux passages consécutifs à zéro et à multiplier par 5,0 µs (puisqu'il y a 5,0 µs par division).
b) calculer l'incertitude U(T) sur la période
On donne quasiment la réponse dans le texte
On considère que l'incertitude U(T) dans la mesure de la période est de 0,2 division
Comme on a 5 µs/div...
Oui, c'est correct... Mais il faut mettre les unités sinon ça ne veut rien dire ou
c) Déterminer la longueur d'onde
 connaissant d. Quelle est l'incertitude U(
connaissant d. Quelle est l'incertitude U( ) sur la longueur d'onde ?
) sur la longueur d'onde ? Le problème est qu'il y a une ambiguïté...
Quand on déplace le récepteur R2, la distance qui sépare deux points consécutifs en phase est égale à
 .
.
D'après toi, dans la distance d, il y a combien de
 ?
? Là, je suis un peu embêté...
Le texte n'est pas suffisamment clair. Je ne sais pas si on compte la première position ou non...
Si on ne compte pas la première position, on a 10  dans la distance d.
dans la distance d.
Si on compte la première position, il n'y en a que 9...
je crois qu'on va prendre 10 ==> d = 10  d'où
d'où 
ok c'est juste ça qu'il faut répondre ? il faut aussi que je calcule l'incertitude U( ) et c'est ça qui me pose le plus problème
) et c'est ça qui me pose le plus problème
L'incertitude sur d est 1 mm. Comme on a d = 10 , l'incertitude sur
, l'incertitude sur  est le 1/10ème de celle sur d ==> 0,1 mm
est le 1/10ème de celle sur d ==> 0,1 mm
d) Quelle est la relation entre la longueur d'onde
 et la période T de l'onde ?
et la période T de l'onde ? Tu dois savoir la réponse... C'est du cours...
Comment as-tu fait pour trouver une période de 32 µs?
Je trouve 5,2 divisions (bien que l'image ne soit pas très claire) donc T = 5,2  5,0 = 26 µs
5,0 = 26 µs
Donc :
Et pour l'incertitude, tu appliques la formule qu'on te donne :
U(v) =  ( (U(
( (U( )/
)/ )2 + (U(T)/T)2 )
)2 + (U(T)/T)2 )
ok je les ferai demain et je verrai merci en tout cas ! je reviens demain sur le forum pour mes autres messages non répondus
Bonjour Manon,
Serait-il possible par curiosité de savoir d'où provient cet exercice; c'est-à-dire de quel livre et quelle édition ?
Je te remercie !



