Inscription / Connexion Nouveau Sujet
Skieur : Déterminer les forces inconnues
Bonjour,
Je suis bloquée à un exercice. Notre cours est partiel et c'est le premier exercice que je fais sur les lois de Newton
Voici l'intitulé :
"le référentiel terrestre est supposé galiléen. Le système étudié est le système skieur+skis. Un skieur de masse 60.0 kg dévale tout droit la pente à vitesse constante.
La réaction normale R(vecteur) (force exercée par le sol sur le système skieur+skis et dont la direction est perpendiculaire au sol). L'angle de la piste est l'horizontale 26°, il caractérise la pente.
a) Démontrer, en vous appuyant sur les lois de Newton, que lors de la descente, la force de frottement ne peut pas être nulle
b) Donner sa valeur arrondie à l'unité. Détailler votre réponse avec rigueur "
Pour le a) j'ai dis que sans force de frottement le skieur à une vitesse qui n'est pas constante donc il y a des forces de frottements (je l'ai évidemment mieux formulé)
Pour le b) je n'y arrive pas, je ne sais pas ce qu'il faut faire
Merci de votre aide et de votre temps
Bonjour,
a) S'il n'y avait pas de force de frottement, effectivement la vitesse ne serait pas constante puisque qu'on aurait une accélération 
qui est une partie de l'accélération de gravité g dépendant de l'angle de la pente
b) Donc la vitesse est constante et l'accélération nulle (bien entendu cela correspond à une situation d'équilibre qui n'est vraie qu'au bout d'un certain temps - en fait en général la force de frottement est une fonction croissante avec la vitesse, ce qui suppose aussi que le skieur et ses skis ne décollent jamais!)
Il faut donc faire l'équilibre des 3 forces (Poids, Réaction du sol, Frottement) auxquelles est soumis le système composé du skieur et de ses skis
A toi de finaliser à partir d'un schéma
Mais du coup la force de frottement est égal à quoi ? F= -P-R ? (P représente le poids et R la force exercée par la sol)
Car sans une formule je ne peux pas calculer
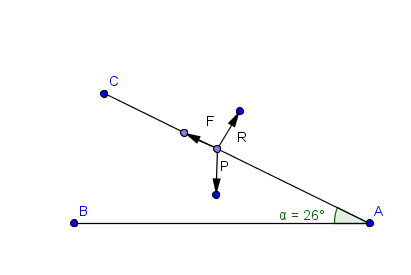
Voici un schéma pour t'aider où il y a un peu de géométrie à faire
Tu dois décomposer le poids P = mg
- suivant l'axe de la pente pour connaître le module de la force F
- suivant l'axe perpendiculaire à la pente pour connaître le module de la force R
A toi de finaliser
Bonsoir,
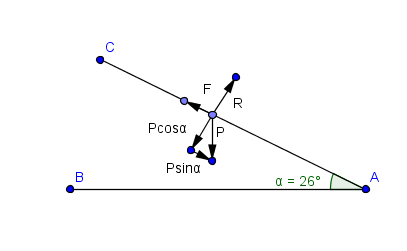
J'ai complété le schéma en montrant la décomposition du poids P
- suivant l'axe de la pente qui s'oppose à F (soit P*sin
)
- suivant l'axe perpendiculaire à la pente qui s'oppose à R (soit P*cos)
Pour rappel on a
Attention il est faux d'écrire que F = -P-R
Ceci n'est vrai que pour les vecteurs mais pas pour les modules des vecteurs
est l'angle de la pente avec l'horizontale : il vaut 26°
C'est aussi l'angle entre la verticale et la perpendiculaire à la pente
On a :
R module de = P * cos(
)
F module de = P * sin(
)
Annuler
connectez vous