Inscription / Connexion Nouveau Sujet
Roulement sans glissement
Bonjour, j'aurais besoin d'aide pour un exercice...
Soit une roue S de centre A et de rayon R qui roule sur un plan, le long de l'axe (O,ex) (la roue reste verticale). R est le référentiel associé au plan.
1 .Soit M un point de la circonférence de la roue. Paramétrer sa position dans R. De combien de paramètre a-t-on besoin à priori ?
2 .Quelle est la vitesse du point M par rapport au sol ?
3 .Donner la vitesse de glissement de la roue par rapport au sol.
4 .En déduire la condition de roulement sans glissement du mouvement de la roue par rapport au sol.On suppose à présent que la roue roule sans glisser sur le plan et on considère un point M de la circonférence de la roue.
5. Donner l'équation paramétrique de la trajectoire et représenter cette courbe.On suppose à présent la vitesse de rotation de la roue par rapport au sol constante, de valeur ω0.
6 .Quelle est la vitesse du point A?
7 .Calculer la vitesse scalaire du point M. En quelle(s) position(s) s'annule-t-elle?
Avant de parler des questions y'a des trucs que je comprends pas...
Qu'est ce que ça veut dire "roulement sans glissement" ? Quand y'a marqué "roule sur un plan, le long de l'axe (O,ex)" Cela veut dire que le bas de la roue est au contact de l'axe (O,ex) ? Et que veut dire "la roue reste verticale" ?
1.Etant donné que la roue tourne, la position de M aussi du coup,non ?
Il a une évolution en x et y. A priori y'a 2 paramètres ?
Bonjour
Pour étudier le mouvement de M, on utilise en général deux coordonnées : l'abscisse du centre d'inertie G de la roue et l'angle entre l'axe Gy et GM.
Cela n'est pas du programme enseignement secondaire...
Ce message pourra peut-être un peu t'aider en adaptant un peu les notations. Il y a roulement sans glissement lorsque la vitesse du point M s'annule quant M passe au contact avec le plan de roulement (lorsque  =0).
=0).
![]() Mouvement Cycloïdal
Mouvement Cycloïdal
Bonjour
Pour étudier le mouvement de M, on utilise en général deux coordonnées : l'abscisse du centre d'inertie G de la roue et l'angle entre l'axe Gy et GM.
Cela n'est pas du programme enseignement secondaire...
Sauf que je ne les ai pas... Et je vois pas comment calculer le centre d'inertie sans avoir de masse...
Il n'y a pas à calculer le centre d'inertie. Pour une roue correctement équilibrée, ce qu'il faut supposer ici, il s'agit du centre de la roue. Les points A et G sont confondus ici.
Voici un schéma qui pourra t'aider. Mais encore une fois : la résolution de cet exercice demande des notions démontrées seulement dans l'enseignement supérieur...
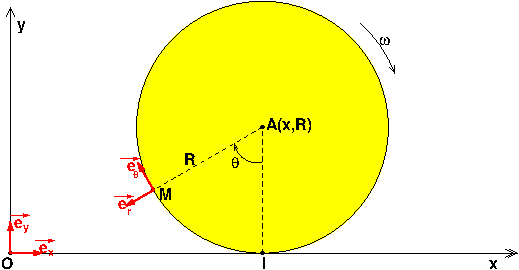
Ah d'accord merci il faut supposer que le centre d'inertie est au centre de la roue... Ensuite mon schéma ressemble presque à celui là. Je n'avais pas pensé à mettre des coordonnées polaires dans le cercle.
Question 2 : la vitesse du point M par rapport à la terre,à une position quelconque repérée par l'angle ,s'écrit :
Dans le cas particulier où M est en I (contact avec le sol), les deux composantes de la vitesses ont la même direction (l'horizontale) mais des sens opposés. La somme vectorielle de ces deux composantes peut donc être nulle pour une valeur particulière de  notée
notée  o.
o.
Imagine une voiture lancée à 80km/h sur une route : imagine la surface du pneu en contact avec la route possédant une vitesse non nulle : le pneu s'userait très rapidement...
Pour la question 1 : j'avais commencé à faire ça :
vecteur OM = vec OI + vec IA + vec AM (Chasles)
= Vt.ex + R.ey + Rer
Vt c'est la vitesse.
R étant une constante connue, les deux paramètres de positions sont :
1° : x : l'abscisse de A que l'on peut éventuellement écrire sous la forme : x=V.t en supposant x= 0 en t=0.
2° : l'angle polaire  défini sur la figure.
défini sur la figure.
Je t'ai déjà fourni la réponse à la question 2.
Je t'ai déjà fourni la réponse à la question 2.
Oui mais je comprends pas la réponse et je suis toujours (bloqué) à la question 1...


