Inscription / Connexion Nouveau Sujet
Roulement d'un wagonnet
Bonjour, svp guidez moi
Problème : Un wagonnet de masse M est monté sur 4 roues de masse m chacune, et de rayon R.
Il est lâché sans vitesse sur un plan incliné de  par rapport au plan horizontal. Le moment d'inertie de chaque roue par rapport à son axe de rotation est J = ½mR². Le wagonnet roule sans glisser suivant la ligne de plus grande pente.
par rapport au plan horizontal. Le moment d'inertie de chaque roue par rapport à son axe de rotation est J = ½mR². Le wagonnet roule sans glisser suivant la ligne de plus grande pente. 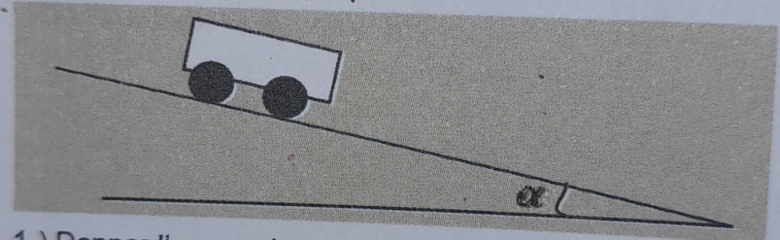
1) Donner l'expression de l'accélération (a) du centre d'inertie du Wagonnet.
2) Quelle doit être la valeur du rapport M/m pour que cette accélération ne différé que de 1/10 de l'accélération qu'il aurait s'il glisser sans rouler sur le même plan incliné.
Bonsoir
Je t'ai expliqué récemment comment exprimer l'énergie cinétique d'un solide en roulement sans glissement.
Bonjour, je reprend ici le problème. Le 1er contient des erreurs de frappe vers la fin.
Problème : Un wagonnet de masse M est monté sur 4 roues de masse m chacune, et de rayon R.
Il est lâché sans vitesse sur un plan incliné de  par rapport au plan horizontal. Le moment d'inertie de chaque roue par rapport à son axe de rotation est J = ½mR². Le wagonnet roule sans glisser suivant la ligne de plus grande pente.
par rapport au plan horizontal. Le moment d'inertie de chaque roue par rapport à son axe de rotation est J = ½mR². Le wagonnet roule sans glisser suivant la ligne de plus grande pente. 
1) Donner l'expression de l'accélération (a) du centre d'inertie du Wagonnet.
2) Quelle doit être la valeur du rapport M/m pour que cette accélération ne diffère que de 1/10 de l'accélération qu'il aurait s'il glissait sans rouler sur le même plan incliné ?
Je pense que le plus simple consiste à appliquer le théorème de l'énergie cinétique, ou la conservation de l'énergie mécanique, pour en déduire l'expression de l'accélération.
D'accord !
1) seuls le poids et la réaction qui sont appliquées sur le système.
Le référentiel terrestre est supposé galiléen.
Le TEc donne :
 Ec= Mgh
Ec= Mgh  Ec - Ec0 = Mgh
Ec - Ec0 = Mgh
Or Ec0 = 0 et Ec = ½Mv² + ½J
 ²
²
Avec J = 4.J = 2mR²
= 4.J = 2mR²
Alors ½Mv² + ½(2mR²) ² = Mgh
² = Mgh
½Mv² + mv² = Mg.x.sin
 (M+2m)v² = 2Mg.x.sin
(M+2m)v² = 2Mg.x.sin
v² = 2[(M.g.sin )/(M+2m)]x
)/(M+2m)]x
D'où
Oui. Tu peux vérifier la cohérence de ton résultat. Si la masse des roues est négligeable devant la masse totale du wagonnet, l'énergie cinétique de rotation est négligeable devant celle de translation et on obtient bien l'accélération "classique" : g.sin( ).
).
PS : pour être rigoureux, il faudrait préciser que les réactions normales ne travaillent par (perpendiculaires à la trajectoire) et que les réactions tangentielles (indispensables, sinon pas de roulement possible) ne travaillent pas non plus car la vitesse des roues s'annulent au contact avec le plan incliné.
D'accord j'ai compris.
Mais comment expliquer (ou démontrer) que la vitesse des roues est nulle au contact avec le plan incliné ?
Si elle ne l'était pas, il y aurait glissement.
Ensuite, démontrer rigoureusement que cette vitesse nulle implique V=R. ,ne peut se faire que niveau (bac+1) même si on peut le comprendre intuitivement plus tôt.
,ne peut se faire que niveau (bac+1) même si on peut le comprendre intuitivement plus tôt.
Merci bien.
2) en appliquant le TCI sur le wagonnet, sachant qu'il glisse sans rouler, on trouve : a' = g.sin
Or "a" differe de " a' " de 1/10, donc : a - a' = 1/10
Alors



