Inscription / Connexion Nouveau Sujet
rotation d'un solide autour d'un axe fixe
Bonsoir svp aidez moi à résoudre ce problème
Un cylindre homogène de rayon r=10cm de masse M=1kg, peut tourner autour de son axe de révolution horizontal D ; il soutient un solide S, de masse m=10kg, par l'intermédiaire d'une corde enroulée sur le cylindre. Le cylindre est traversé suivant un diamètre par une tige t (figure) portant à ces extrémités deux masses égales, de valeur m'=0,5kg ,pratiquement confondues à leurs centres de gravité situés à l=50cm de l'axe D. Le système est abandonné sans vitesse initiale.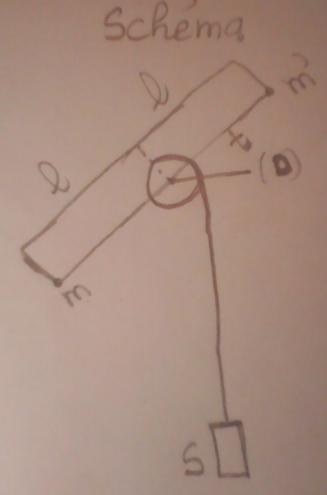
1) En négligeant les masses de la corde et de tige t ainsi que les résistances passives, calculer l'accélération de S et la tension de la corde pendant ce mouvement.
2) La corde quitte le cylindre quand S est descendu de h=5m ; calculer la vitesse angulaire du cylindre à cet instant ( en rad/s et tours/minute) et le nombre de tours effectués par le cylindre depuis le départ. On donne g=10 SI.
--------------
voici mon début
S est en translation donc d'après le TCI on a : P-t=ma => t=mg-ma
le cylindre et la tige sont en rotation
je suis bloqué à ce niveau. comment déterminé t
***Sujet remanié***
Bonjour,
1. Tu as deux inconnues à déterminer : la tension du fil et l'accélération, il faut donc deux équations ...
Bonjour,
Quel est l'équivalent de F=ma pour un solide en rotation ? Pistes :
- il faut remplacer l'accélération linéaire a par l'accélération angulaire
- moment d'inertie
- moment d'une force
+M=somme des moments
nous avons +M=J(D)*α''
pour le cylindre on a :
P*r+t'*r=J(D) *α'' et α''=a/r =>
P*r+r*t'=J(D)*a/r => t'=J(D)*a/r-P*r
J(D)=1/2mr² => t'= 1/2mr²*a/r-mgr
pour la tige
P'*r-P'*r=J(D) *α''=0 => +M=0
la somme des moments de la tige est nulle est ce que je peux égaler les tensions( t et t') et ensuite tirer a ?
L'idée de base est bien la bonne. Mais il y a des choses à améliorer.
La première chose à faire est d'ajouter sur votre schéma les forces qui s'appliquent d'une part à S, d'autre part au cylindre, ce qui permettra d'écrire correctement M.
La deuxième chose, qui va plutôt simplifier, est de considérer le cylindre et la tige comme un seul solide ("Le cylindre est traversé ...).
Ensuite pour la relation entre t et t', la réponse est contenu dans "En négligeant les masses de la corde...".
Attention aux notations : m est la masse de S, la masse du cylindre est M et les masselottes m'.
Deuxième chose : J(D)=1/2Mr² pour le cylindre seul, il faut aussi tenir compte des masselottes.
Troisième chose : a=r*α'', OK, mais il faudra rédiger avec un dessin, des angles orientés et un axe z orienté.
Après correction des points ci-dessus, il ne reste plus que t, t'.
Ahh ! Oui c'est vrai
moment d'inertie
J(D) = 1/2Mr²+2ml²
t'=( 1/2Mr²+2ml²)*(a/r)/r
t=(4ml²+Mr²)/2*a/r² mais pour le dessin faudra que
Vous prenez votre dessin, vous mettez un axe vertical Oz vers le bas (vous avez écrit +mg), vous placez , vous indiquez le sens positif de
compatible avec votre t'*r =J*α''. Ensuite montrez que lorsque augmente, z en fait autant, ce qui traduit en vitesse donne r'=z'.
C'est bien à un détail près, t' est la tension de la corde, donc n'est pas placée au bon endroit, vous avez vous-même écrit que son moment était t'*r.
OK ! t' est sur la corde
vous avez ensuite dit que lorsque α augmente z en fait autant ce qui traduit rα'=z'.comment ?
C'était juste pour vérifier/justifier le signe, comme vous avez écrit spontanément a=r*α'', ce qui est correct, je voulais juste signaler le problème éventuel de signe.
Si α augmente (α'>0), z en fait autant (z'>0) donc on bien le bon signe rα'=z'.
S est soumis à son poids P et l'action de la corde t.
Réciproquement la corde est soumise à -t.
Pour la corde on a donc t'-t=m(corde)*a, mais "négligeant les masses de la corde", m(corde)=0, et donc ?
la tension de la corde pendant ce mvt : t=t'=mg-ma => t=72N
2) h=5m
la vitesse angulaire à cet instant
V=r*w => w= V/r et v=√2ah
w=(√2ah)/r et après tout calcul
w=53 rad/s
tours/min c'est l'unité de la fréquence non ?
C'est bien tout çà : vous vous répondez à vous même !
Sinon pour le nombre de tours, vous avez écrit α''=a/r , autrement dit α'=v/r ou encore α=h/r (avec des origines nulles pour l'angle et la hauteur).
Donc vous avez α, l'angle dont a tourné le cylindre, il y a juste à convertir en tours.
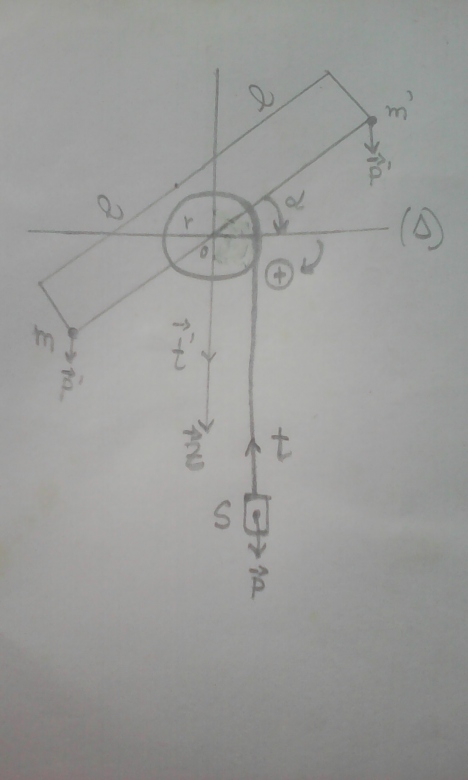
, il a fait combien de tours ?
Annuler
connectez vous