Inscription / Connexion Nouveau Sujet
Robot à câble
Bonjour,
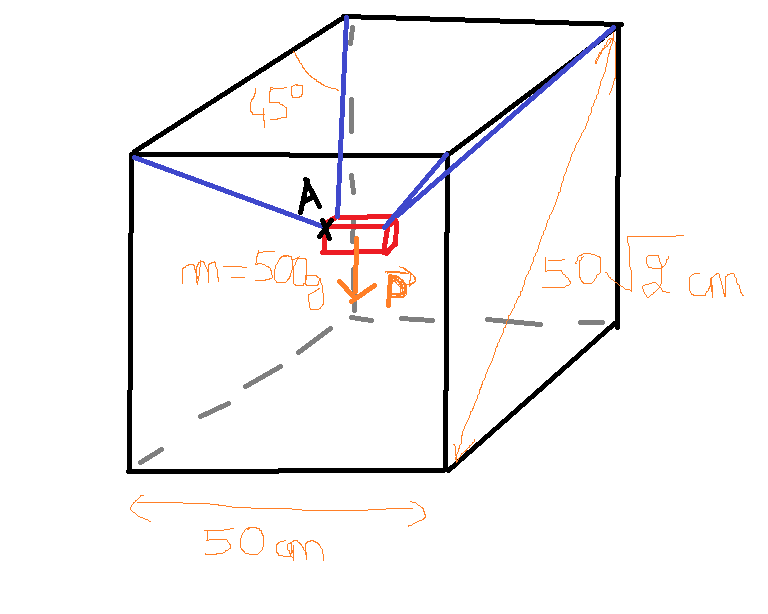
j'ai un projet en cours où je dois réaliser un robot à câble. Un objet quelconque de masse M=500g sera suspendue dans la vide accrocher par 4 câbles au quartes points en haut de l'objet. Les câbles étant eux même accrocher à une structure avec un angle de 
entraîner par des servos moteurs à l'aide d'une poulie. Pour nos écars théorique nous devons calculer la tension des câbles à un point A.
Pour que cela soi plus facile on c'est dit de mettre l'objet au centre de la structure pour que les câbles exerces tous la même tension ( comme ça on en calcule une et on la divise par 4?). On admet donc un angle =45°
On a vu plusieurs calculs sur le net mais aucun qui correspondait à notre cas. Est ce que vous savez comment l'on pourrait faire? 
Merci 
Hello
Un peu flou ton dispositif. En supposant que la structure est cubique et que les câbles aient à l'équilibre même longueur, alors l'équilibre de la masse m se traduit par:
donc
Bonjour,
Si j'ai bien compris le problème posé par jeanne 44400
La condition d'équilibre ne serait elle pas :
plutôt que
même si pour des raisons de symétrie T1 =T2 = T3 =T4
Alors on en revient au flou que tu évoquais.
Il y a une contradiction entre la figure ou les tensions n'ont pas la même direction et l'affirmation :
les câbles exerces tous la même tension
Mais peut jeanne44400 voulait elle dire :
Les câbles exercent tous des tensions de même intensité.
Je présume (à cause des servo moteurs) qu'il s'agit de monter ou descendre la charge en modifiant en même temps les longueurs des 4 câbles (par les servo moteurs)
Si oui, alors l'angle de 45° indiqué ne rime à rien.
Supposons le cube de coté a, on peut donc faire bouger la masse (par modification des longueurs des 4 câbles par servo-moteurs) depuis la base basse jusqu'au sommet (au presque)
Soit h la distance entre la base basse du cube et la masse (supposée ponctuelle pour faciliter les calculs).
En posant X = h/a :
On trouve (sauf erreur très possible, pas vérifié) que la tension dans chacun des 4 câbles est :
(hors efforts dynamiques)
Qui pour le cas où X --> 1 (donc masse tout en haut), on aurait T infini.
(Ce qui est normal, car les câbles sont alors dans un plan horizontal et sont donc incapables de vaincre le poids (vertical))
Calculs à refaire ... bien évidemment
Il me semble qu'il y a une erreur dans mes calculs, car au pif, T pour X --> -oo devrait valoir P/4
Peut être :
Il reste à vérifier.
C'est vrai que je ne devais pas être bien réveillé ce matin pour sortir une telle ânerie...
En toute rigueur, il faudrait connaitre les dimensions de l'objet pour calculer T en fonction de x/a.
Mais en supposant l'objet quasi ponctuel (de dimension << 50 cm), et h pouvant varier de 0 à a ... je trouve comme J-P ... c'est rassurant ... pour moi 
Pour jeanne:
- d'un côté (et non pas 4T = P
)
- de l'autre si tu appelles l'angle entre une arête verticale et le câble qui s'y rattache:
avec (c'est là que le quasi ponctuel intervient)
en développant tu arrives au résultat établi par J-P
(obbugt1, ton "hum hum" était trop soft, avec les ânes il faut jouer du bâton plus fort ...)
Je me suis lancé, moi aussi, dans le calcul de T en employant la même hypothèse simplificatrice d'un objet ponctuel et le même changement de variable que JP soit X=h/A
J'ai trouvé :
donc le même résultat que JP à un signe près.
Exact.
Erreur de débutant de ma part.
J'ai sorti (X-1)² du dénominateur de la racine carrée ... et oublié les valeurs absolues.
Il me semble qu'il y a une erreur dans mes calculs, car au pif, T pour X --> -oo devrait valoir P/4
Peut être :
Il reste à vérifier.
Merci J-P pour votre réponse. Pouvez vous m'expliquez comment trouvez vous ce calcule de T car c'est là que je bloque, car j'ai trouvé que T=P/4sin(a)
Et est ce que P=m? C'est a dire le poid de notre cube, 500g?
Nous avons pris un cube avec h=10 et a=20, ce qui nous donne X=0.5, avec votre formule je trouve T=306,186 (environ et en prenant 1-X au lieu de X-1, comme l'a dit odbugt1
), est ce que je cela est probable?En considérant 2 coins du cube situés sur une même diagonale de la face supérieure.
Les cordes passant par ces 2 points et le centre de gravité de la masse (supposée ponctuelle) sont dans un même plan vertical.
Pour raison de symétrie, ces 2 cordes compensent le demi poids de la pièce (l'autre moitié est compensée par les 2 cordes partant des 2 autres coins)
on a donc ceci :
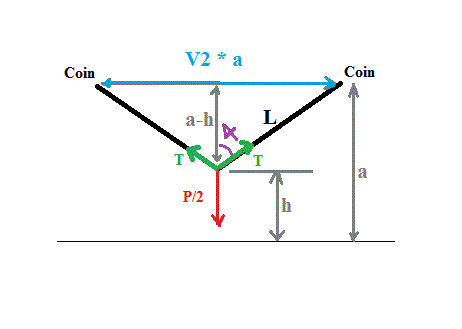
L² = (a-h)² + a²/2
L = V((a-h)² + a²/2)
cos(alpha) = (a-h)/L = (a-h)/V((a-h)² + a²/2)
Projection des forces sur un axe vertical :
P/2 = 2T.cos(alpha)
T = P/4 * V((a-h)² + a²/2)/(a-h)
En divisant numérateur et dénominateur par a et posant X = h/a, il vient :
T = P/4 * V((1-X)² + 1/2)/(1-X)
T = P/4 * V(X²-2X + 3/2)/(1-X)
T = P/4 * V((2X²-4X + 3)/2)/(1-X)
Sauf distraction.
Et donc par exemple, pour une masse de 500 g
P = 0,5 * 10 = 5 N (en prenant g = 10 N/kg)
-----
Si la charge se trouve à h = a/2 (milieu du cube)
alors X = 1/2
La tension dans chacune des cordes est :
T = P/4 * V((2X²-4X + 3)/2)/(1-X)
T = 5/4 * V((2 * 1/4 - 4/2 + 3)/2) / (1 - 1/2)
T = 5/4 * V(0,75) /0,5 = 2,165 N
----
Si la charge se trouve à h = 0+ (presque sur le sol)
alors X = 0
La tension dans chacune des cordes est :
T = 5/4 * V(3/2)/(1-0) = 1,53 N
----
Si la charge se trouve à h = 3a/4
alors X = 3/4
La tension dans chacune des cordes est :
T = 5/4 * V((2*0,75²-4*0,75+ 3)/2)/(1-0,75)
T = 3,75 N
----
Si la charge est tout en haut (a = h)
... C'est impossible car on aurait T = +oo.
-----
Tout ceci, si la charge est ponctuelle ou quasi (si on peut considérer ses dimensions comme < < que a)
Sauf distraction. (calculs non vérifiés).
Annuler
connectez vous